サンプル

第六章　行列とベクトル

§1. 行列と行列式

　我々は小学校で $2$ や $3$ という日常的に使う“普通の数”を知る。前章で学んだ「複素数」は実数と虚数という二種類の数を持ち、次節で学ぶ「ベクトル」は一般に二つ以上の“普通の数”を持つ。さらに多い“普通の数”を持つ「行列」がある。これら“普通の数”“複素数”“ベクトル”“行列”などはすべて数学上の“数”である。すなわち“数”にはたくさんの種類がある。（以降、“数”を構成する“普通の数”の個数を「成分」と言う。）行列と似た名前を持つ数に「行列式」がある。名前は似ているが「行列」と「行列式」はまったく異なる数である。行列は「“普通の数”の集まり」であり、行列式は「一つの“普通の数”」を表す。
　小学校では“普通の数”の「四則演算（足し算、引き算、掛け算、割り算）」を学ぶが、「複素数」「行列」「行列式」「ベクトル」などの数に対しても「四則演算」が存在し、それらの規則は少しずつ違う[1]。しかし、それらの数の成分が一つの場合には「四則演算」は全て同じになり、すでに知っている“普通の数”の「四則演算」に帰着する。
　なぜ数の概念を日常的には使わない複素数やベクトルなどという数にまでひろげて考えるのか不思議に思うに違いない。その答えは自然科学の歴史が教えてくれる。すなわち、数の概念を含め一つのことをより広い観点から異なるやり方で理解すると、しばしば新しい発見があり、それが新しい恵みを我々の世界にもたらすことを長い科学の歴史が教えてくれているからである。もし全ての科学に共通する考え方があるとすれば、この「より広い観点から考えること」であると言えるだろう。普通の数の概念を複素数、ベクトル、行列などに広げて考えるのも「より広い観点から考えること」の一つである。この章ではそのなかの「行列」と「行列式」について学び、続いて「ベクトル」について学ぶ。

【行列】

　まず行列を定義することから始める。行列はその名が示す通り、数（要素）が横の行と、縦の列に並んだ数の集まりである。たとえば

<6-1>　(6.1.1)　 $(\begin{matrix} 1 & 5 & 2 \\ 4 & 2 & 3 \end{matrix})$

は $2$ 行 $3$ 列の行列である。一般に横の並びが $N$ 行、縦の並びが $M$ 列の行列を $N 行 M 列$ の行列、あるいは $N \times M$ 行列という。このとき各位置にある数をこの行列の要素（行列要素）という。(6.1.1)式の行列は $2 行 3 列$ の行列（または $2 \times 3$ 行列）である。
　行数と列数が同じ行列を「正方行列」といい、物理では最も多く現れる行列である。以下に行列が有するいくつかの重要な性質を列挙するが、あるものは正方行列でしか成り立たない性質もあるので、それはその都度ことわることにする。

【行列の等式】 二つの行列 $A$ と $B$ について、
① $A$ の行数と $B$ の行数、 $A$ の列数と $B$ の列数が一致し、すべての行列要素が等しいときにのみ $A$ と $B$ は等しく、それを $A = B$ と書く。
② もし $A = B$ なら、 $A$ と $B$ の行列要素は全て等しい。
【行列の和と差】 $N_{1} 行$ $M_{1} 列$ の行列と $N_{2} 行$ $M_{2} 列$ の行列はそれらの行数と列数が同じとき、すなわち $N_{1} = N_{2}$ および $M_{1} = M_{2}$ のときにのみ、それらを加えたり引いたりすることができる。その加減の規則は
<6-2>　(6.1.2)　 $\begin{matrix} (\begin{matrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \end{matrix}) \pm (\begin{matrix} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \end{matrix}) \\ = (\begin{matrix} a_{11} \pm b_{11} & a_{12} \pm b_{12} & a_{13} \pm b_{13} \\ a_{21} \pm b_{21} & a_{22} \pm b_{22} & a_{23} \pm b_{23} \end{matrix}) \end{matrix}$
によって与えられる。
【行列の定数倍】 行列の定数 $(k)$ 倍は、行列の各要素が定数倍された行列になる。すなわち
<6-3>　(6.1.3)　 $k (\begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix}) = (\begin{matrix} k a_{11} & k a_{12} \\ k a_{21} & k a_{22} \end{matrix})$
である。
【行列の積１】ある列数を持つ行列に、その列数と同じ行数を持つ行列を右からかけることができる。すなわち、 $N \times L 行列 A$ に $L \times M 行列 B$ をかけることができる。詳しく書くために $A$ と $B$ の行列要素を
$\begin{matrix} <6-4> A = (\begin{matrix} a_{11} & a_{12} & \dots & a_{1 L} \\ a_{21} & a_{22} & \dots & a_{2 L} \\ \dots & \dots & \dots & \dots \\ a_{N 1} & a_{N 2} & \dots & a_{NL} \end{matrix}) \\ <6-5> B = (\begin{matrix} b_{11} & b_{12} & \dots & b_{1 M} \\ b_{21} & b_{22} & \dots & b_{2 M} \\ \dots & \dots & \dots & \dots \\ b_{L 1} & b_{L 2} & \dots & b_{LM} \end{matrix}) \end{matrix}$
とし、積 $A \times B$ で出来あがる行列を $C$ とすれば、
<6-6> $\begin{matrix} C = (\begin{matrix} c_{11} & c_{12} & \dots & c_{1 M} \\ c_{21} & c_{22} & \dots & c_{2 M} \\ \dots & \dots & \dots & \dots \\ c_{N 1} & c_{N 2} & \dots & c_{NM} \end{matrix}) \end{matrix} であり、 A と B の行列要素を使ってその行列要素を表せば、$
<6-7>　(6.1.4)　 $\begin{matrix} \{\begin{matrix} c_{11} = a_{11} b_{11} + \dots + a_{1 L} b_{L 1} \\ c_{12} = a_{11} b_{12} + \dots + a_{1 L} b_{L 2} \\ \dots \\ c_{1M} = a_{11} b_{1 M} + \dots + a_{1 L} b_{LM} \end{matrix} \\ \{\begin{matrix} c_{21} = a_{21} b_{11} + \dots + a_{2 L} b_{L 1} \\ c_{22} = a_{21} b_{12} + \dots + a_{2 L} b_{L 2} \\ \dots \\ c_{2M} = a_{21} b_{1 M} + \dots + a_{2 L} b_{LM} \end{matrix} \\ \dots \\ \{\begin{matrix} c_{N1} = a_{N 1} b_{11} + \dots + a_{NL} b_{L 1} \\ c_{N2} = a_{N 1} b_{12} + \dots + a_{NL} b_{L 2} \\ \dots \\ c_{NM} = a_{N 1} b_{1 M} + \dots + a_{NL} b_{LM} \end{matrix} \end{matrix}$
である。行列の積に関しては、普通の数にはない非常に特徴的で重要な性質がある。すなわち、もし二つの正方行列 $A$ と $B$ が同じ行数（および列数）を持てばそれらの積 $AB$ と $BA$ が作れ、結果はともに同じ行数と列数を持つ正方行列となって $AB$ は $BA$ の行と列を入れ替えた行列になるが、一般に $AB \neq BA$ である。これは非常に重要な行列の積の性質である。（「不確定性原理」という言葉をどこかで聞いたことがあるかもしれない。「不確定性原理」は全ての現代物理学の基礎を構成する「量子力学」の基本的原理であるが、その数学的な表現が行列の積に関するこの性質と密接な関係がある。）
【転置行列】 ある行列 $A$ に対して、その行と列を入れ替えた行列の必要になることがある。そのような行列を $A$ の転置行列といい $A^{T}$ と記す：
<6-8>　(6.1.5)　 $A = (\begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{matrix}) とするとき A^{T} = (\begin{matrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{matrix})$
である。 $(N \times L)$ 行列 $A$ と $(L \times M)$ 行列 $B$ の積 $AB$ は $(N \times M)$ 行列になるが、それを転置した $(M \times N)$ 行列 ${(AB)}^{T}$ は、 $B$ の転置行列である $(M \times L)$ 行列 $B^{T}$ と $A$ の転置行列である $(L \times N)$ 行列 $A^{T}$ の積に一致する。すなわち
<6-9>　(6.1.6)　 ${(AB)}^{T} = B^{T} A^{T}$
である。適当な行列 $B$ を自分で作り、(6.1.5)式で与えた行列 $A$ との積を使って各自で確かめるとよい。
【対角行列と単位行列】 対角要素以外の要素が $0$ である正方行列を対角行列という。特に全ての対角要素が $1$ でそれ以外の要素が $0$ である対角行列
<6-10>　(6.1.7)　 $E = (\begin{matrix} 1 & 0 & 0 & \dots \\ 0 & 1 & 0 & \dots \\ 0 & 0 & 1 & \dots \\ \dots & \dots & \dots & \dots \end{matrix})$
を単位行列という。 $1$ ではない同じ数（たとえば $a$ が対角要素に並ぶ行列）に対しては、その行列を $(1 / a)$ 倍することによって単位行列に作り変えることができる。
【単位行列の性質】 任意の正方行列 $A$ にそれと同じ行（列）数を持つ単位行列をかけても、生じる行列は元の行列と変わらない。すなわち
<6-11>　(6.1.8)　 $AE = EA = A$
である。
【零行列】 全ての要素が $0$ の正方行列：
<6-12>　(6.1.9)　 $O = (\begin{matrix} 0 & 0 & \dots \\ 0 & 0 & \dots \\ \dots & \dots & \dots \end{matrix})$
を零行列という。どのような正方行列にそれと同じ行（列）数を持つ零行列を加えても行列は変わらず、どのような正方行列でもそれに同じ行（列）数を持つ零行列をかけると零行列となる。
【逆行列】 0でない任意の数 aに掛けて、その結果が1 となる数をaの逆数といい、 1aあるいはa- 1と書く。すなわち、
<6-13>　 $\frac{1}{a} a = a^{- 1} a = 1$
である。
　逆数と同じように、零行列でない任意の正方行列 $A$ に対して、その行列要素を使って計算される「行列式」とよばれる数が $0$ でなければ、
<6-14>　 $A B = B A = E$
であるような行列 $B$ が存在し、 $B$ を $A$ の逆行列と呼んで $A^{- 1}$ と書く。すなわち、もし $A$ に逆行列があれば
<6-15>　(6.1.10)　 $A A^{-1} = A^{-1} A = E$
である。逆行列はこの後に学ぶ連立方程式で非常に重要な役割を果たす。
　ある正方行列を与えたとき、その逆行列を作ることはそれほど簡単ではない。その難しさは行列の行数が増すにつれて増すが、行数が少なければ比較的容易に逆行列を作ることができ、その有用性を理解することができる。具体例を一つ示す。もし $A$ が $2 \times 2$ の行列
<6-16>　 $A = (\begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix})$
であれば、この逆行列は
<6-17>　 $A^{-1} = \frac{1}{det (A)} (\begin{matrix} a_{22} & - a_{21} \\ - a_{12} & a_{11} \end{matrix})$
で与えられる。ここで $det (A)$ が(6.1.10)式上の説明に逆行列が存在する条件として現れた $A$ の「行列式」とよばれる量であり、具体的には
<6-18>　 $det (A) = a_{11} a_{22} - a_{12} a_{21}$
で与えられる。実際にこの $A^{-1}$ が(6.1.10)式を満足していることは容易に確かめられる。
　一般に $m \times m$ 正方行列
<6-19>　(6.1.11)　 $M = (\begin{matrix} p_{11} & p_{12} & \dots & p_{1 m} \\ p_{21} & p_{22} & \dots & p_{2 m} \\ \dots & \dots & \dots & \dots \\ p_{m 1} & p_{m 2} & \dots & p_{mm} \end{matrix})$
に対して、その行列式は同じ行列要素を用いて与えられる数であり、
<6-20>　(6.1.12)　 $det (M) = |\begin{matrix} p_{11} & p_{12} & \dots & p_{1 m} \\ p_{21} & p_{22} & \dots & p_{2 m} \\ \dots & \dots & \dots & \dots \\ p_{m 1} & p_{m 2} & \dots & p_{mm} \end{matrix}|$
のように書かれる。重要なことなので強調するが
- 行列がいくつかの数の集まりであるのに対して行列式は一つの数である
　行列式を行列から計算する一般的な計算規則はあるが、それはかなり煩雑なので与えることはしない。ここでは最も普通に使われる 2×2行列と 3×3行列の結果だけを与えておく。もし一般論が必要なら数学の教科書を参照してほしい。
　2×2行列に対する行列式は
<6-21> (6.1.13) $\begin{matrix} det (M_{2}) \equiv |\begin{matrix} p_{11} & p_{12} \\ p_{21} & p_{22} \end{matrix}| \\ = p_{11} p_{22} - p_{12} p_{21} \end{matrix}$
であり、 $3 \times 3$ 行列に対する行列式は
<6-22>　(6.1.14)　 $\begin{matrix} det (M_{3}) \equiv |\begin{matrix} p_{11} & p_{12} & p_{13} \\ p_{21} & p_{22} & p_{23} \\ p_{31} & p_{32} & p_{33} \end{matrix}| \\ = p_{11} p_{22} p_{33} + p_{12} p_{23} p_{31} + p_{13} p_{21} p_{32} \\ - p_{13} p_{22} p_{31} - p_{12} p_{21} p_{33} - p_{11} p_{23} p_{32} \end{matrix}$
である。前ページに与えた $2 \times 2$ 行列 $A$ の $det (A)$ が(6.1.13)式の $det (M_{2})$ から計算される結果と一致していることを確認してほしい。
　多数の行数あるいは列数を持つ行列の行列式を計算する一般規則もあるが、 $2 \times 2$ 行列と $3 \times 3$ 行列以外はそれを具体的に書き下すのは大変である。幸い近年は電子計算機の発達で、どのように大きな行列に対しても、その行列式を瞬時に計算することができるようになり、したがって多くの要素を持つ行列の逆行列を与えることにも何の問題もなくなった。
【対称行列と反対称行列】 転置行列が元の行列と同じ行列（ $A^{T} = A$ なる行列）を対称行列、元の行列と符号が反転している行列（ $A^{T} = - A$ なる行列）を反対称行列という。反対称行列の対角要素が $0$ であることは理解できるであろう。
【隋伴行列とエルミート行列】 少し面倒な概念であるが、行列に関して最も重要な操作の一つにエルミート共役を作る操作がある。これはどうしても理解しないといけない重要な操作である。この重要さが分かるには「量子力学」を学ぶまで待たないといけない。
　ある行列Aのエルミート共役を作るとは Aに対して次の二つの操作を行うことである。
1. $A$ の全ての行列要素の複素共役を作る、すなわち要素が虚数単位 $i$ を持っていればそれを $- i$ とする。そのようにして $A$ から作られる行列を $\bar{A}$ と書く。
2. $A$ の全ての行と列を入れ替える（転置行列を作る）。そのようにして $A$ から作られる行列を $A^{T}$ と書く。
1と2の操作を実行してできた行列をAの隋伴行列といい A*と書く[2]。二つの操作はどちらから先に行っても同じ結果になる：
<6-23>　(6.1.15)　A*=(A ¯)T=(AT) ¯
重要なことであるから実例をいくつかあげる。今Aを 2×2行列
<6-24>　 $A = (\begin{matrix} cos θ & sin θ \\ - sin θ & cos θ \end{matrix})$
とする。これに対して $A^{*}$ は
<6-25>　 $A^{*} = (\begin{matrix} cos θ & - sin θ \\ sin θ & cos θ \end{matrix})$
である。したがって $A^{*} \neq A$ である。一方 $2 \times 2$ 行列
<6-26>　 $H = (\begin{matrix} cos θ & i sin θ \\ - i sin θ & cos θ \end{matrix})$
に対して $H^{*}$ は
<6-27>　 $H^{*} = (\begin{matrix} cos θ & i sin θ \\ - i sin θ & cos θ \end{matrix})$
なので $H^{*} = H$ である。このように隋伴行列が元の行列に一致する行列を「エルミート行列」という。 $H$ はエルミート行列であるが、 $A$ はエルミート行列ではない。
　エルミート行列 $M = M^{*}$ の対角線を挟んだ対称の位置にある行列要差は互いに複素共役の関係にある。すなわち $M$ の $i$ 行 $j$ 列要素を $M_{ij}$ とすると、 $M_{ij} = (M_{ji})^{*}$ である。
【行列の積２】 上に与えた行列 $A$ の他にもう一つの行列 $B$ を
<6-28>　 $B = (\begin{matrix} 0 & 2 \\ 1 & 0 \end{matrix})$
とする。これから二種の行列の積 $AB$ と $BA$ をつくると
<6-29>　 $\{\begin{matrix} AB = (\begin{matrix} sin θ & 2 cos θ \\ cos θ & - 2 sin θ \end{matrix}) \\ BA = (\begin{matrix} - 2 sin θ & cos θ \\ cos θ & sin θ \end{matrix}) \end{matrix}$
であるから、明らかに $AB \neq BA$ である。
　また
<6-30>　 $\begin{matrix} A^{T} = (\begin{matrix} cos θ & - sin θ \\ sin θ & cos θ \end{matrix}) \\ B^{T} = (\begin{matrix} 0 & 1 \\ 2 & 0 \end{matrix}) \end{matrix}$
であるから
<6-31>　 $\begin{matrix} (AB)^{T} = (\begin{matrix} sin θ & cos θ \\ 2 cos θ & - 2 sin θ \end{matrix}) \\ B^{T} A^{T} = (\begin{matrix} sin θ & cos θ \\ 2 cos θ & - 2 sin θ \end{matrix}) \end{matrix}$
であり、したがって
<6-32>　 $(AB)^{T} = B^{T} A^{T}$
が成り立つ。これは一般の正方行列に対して成り立つ。
　この節の冒頭に、「我々が行列を学ぶ前に知った“普通の数”は行列の特別な場合に含まれる。」と書いた。“普通の”数 $a$ は一行一列の行列で本来なら行列として $(a)$ と書くべきであろうが、この場合には行と列を取り違えることもなく、二つの行列の積が掛ける順番によって異なることもない。したがって、それが行列であることを示すためにかっこで囲む必要もないので、単に $a$ と書いても構わない。以後も普通の数の時はこれまでのようにかっこのない普通の書き方で表す。容易に確かめることができるように、行列が“普通の数”の場合にも上述した全てのことが成り立つ。

【行列式と連立一次方程式】
　 $x$ と $y$ に関する次の連立一次方程式を解こう。
<6-33>　(6.1.16)　 $\begin{matrix} \{\begin{matrix} a_{11} x + a_{12} y = b_{1} \\ a_{21} x + a_{22} y = b_{2} \end{matrix} \\ ただし a_{11} a_{22} - a_{12} a_{21} \neq 0 とする。 \end{matrix}$
面倒だが落ち着いて解けば、その結果は
<6-34>　(6.1.17)　 $\begin{matrix} x = \frac{a_{22} b_{1} - a_{12} b_{2}}{a_{11} a_{22} - a_{12} a_{21}} \\ y = \frac{a_{11} b_{2} - a_{21} b_{1}}{a_{11} a_{22} - a_{12} a_{21}} \end{matrix}$
となる。与えられた条件から分母が $0$ でないことに注意してほしい。
　この面倒な方程式を行列を使って簡単に解く方法がある。まず次の三つの行列を用意する：
<6-35>　(6.1.18)　 $\begin{matrix} A = (\begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix}) \\ X = (\begin{matrix} x \\ y \end{matrix}) \\ B = (\begin{matrix} b_{1} \\ b_{2} \end{matrix}) \end{matrix}$
$A$ は(6.1.16)式の $x$ と $y$ の係数から作られる行列、 $X$ は連立方程式の未知数をたてに並べて作った行列、 $B$ は(6.1.16)式右辺をたてに並べて作った行列である。この三つの行列から等式
<6-36>　(6.1.19)　 $AX = B$
を作り両辺の要素を等しく置けば、それは(6.1.16)式と完全に一致する。つまり、(6.1.19)式の行列等式と(6.1.16)式の連立方程式は等価である。
　そこで(6.1.19)式の両辺に左から $A$ の逆行列 $A^{- 1}$ をかける。 $A^{- 1} A = E$ 、 $EX = X$ であるから、その結果は
<6-37>　(6.1.20)　 $X = A^{- 1} B$
である。　しかるに $A^{- 1}$ は
<6-38>　(6.1.21)　 $A^{- 1} = [det(A {)]}^{- 1} (\begin{matrix} a_{22} & - a_{12} \\ - a_{21} & a_{11} \end{matrix})$
であり、<6-39> $(det(A) = a_{11} a_{22} - a_{12} a_{21})$ であったから、(6.1.20)式は
<6-40>　(6.1.22)　 $X = \frac{1}{a_{11} a_{22} - a_{12} a_{21}} (\begin{matrix} a_{22} b_{1} - a_{12} b_{2} \\ - a_{21} b_{1} + a_{11} b_{2} \end{matrix})$
となる。(6.1.22)式右辺の二つの成分を $X$ の成分と等しく置けば
<6-41>　(6.1.23)　 $\begin{matrix} x = \frac{a_{22} b_{1} - a_{12} b_{2}}{a_{11} a_{22} - a_{12} a_{21}} \\ y = \frac{a_{11} b_{2} - a_{21} b_{1}}{a_{11} a_{22} - a_{12} a_{21}} \end{matrix}$
を得る。この式は(6.1.16)式の連立方程式を解いた結果と完全に一致する。
　このように、もし方程式の係数が作る行列の逆行列（(6.1.21)式）が存在すれば、それを使って連立一次方程式を必ず解くことができる。すなわち元の方程式で求める未知数がいくつあっても(6.1.20)式は成り立つ。ただし(6.1.21)式右辺にある行列式 $[det(A)]$ が $0$ であれば逆行列が存在しないので、その場合は連立一次方程式も解けず、方程式に解は存在しない。このような時は何が起きていてどのようにすれば良いかは、この節の最後に述べることにする。
　実際に、現実の世界で複雑な現象（気象予報や地震予知もその中に入る）を扱う時に現れる連立方程式は膨大な数の未知数を持ち、人力でそれを間違えなく処理することはどれほど時間をかけても不可能に近い。その場合でも行列を使い形式的な解を(6.1.20)式のように簡単に与えることができる。その内容を具体的に得るためには逆行列と行列の掛け算が必要になるが、それはコンピューターで驚くほど短時間で処理することができる[3]。
　その意味で、 $N$ 個の未知数 $(x_{1}, x_{2}, \dots, x_{N})$ を持つ連立一次方程式
<6-42>　(6.1.24)　 $\{\begin{matrix} a_{11} x_{1} + a_{12} x_{2} + \dots + a_{1 N} x_{N} = b_{1} \\ a_{21} x_{1} + a_{22} x_{2} + \dots + a_{2 N} x_{N} = b_{2} \\ \dots \\ a_{N 1} x_{1} + a_{N 2} x_{2} + \dots + a_{NN} x_{N} = b_{N} \end{matrix}$
の一般的な解は(6.1.20)式と同じ
<6-43>　(6.1.25)　 $X = A^{- 1} B$
である。ただし、今の場合は
<6-44>　(6.1.26)　 $\begin{matrix} X = (\begin{matrix} x_{1} \\ x_{2} \\ \dots \\ x_{N} \end{matrix}) \\ A = (\begin{matrix} a_{11} & a_{12} & \dots & a_{1 N} \\ a_{21} & a_{22} & \dots & a_{2 N} \\ \dots & \dots & \dots \\ a_{N 1} & a_{N 2} & \dots & a_{NN} \end{matrix}), B = (\begin{matrix} b_{1} \\ b_{2} \\ \dots \\ b_{N} \end{matrix}) \end{matrix}$
であり、 $det(A) \neq 0$ とする。

　最後に

det(A) = 0

となる場合について触れておこう。この場合には解が求まらない。このようなことが起きる場合のほとんどは、元の方程式のいくつかが同じであって、解を求めるために方程式の数が不足している場合である。しっかりと理解されない、当たり前のことがある。

一連の未知数を含む方程式から未知数を決定するには、方程式の数は未知数と同じか多くなければならない。

したがって

det(A) = 0

となった時は、独立な方程式の総数が未知数の数と同じになるよう、元の方程式のどれとも異なる方程式を与えなければならない。独立な方程式の総数が多い時は別な問題がおきるが、それは述べずにおく。

§2. ベクトルと行列

　自然界に存在する物理量には、大きさだけを持つ「スカラー」量と、空間的な向きのある「ベクトル」量がある。実際には他の性質を持つ量もあるが当面知る必要はない。「スカラー」量は大きさを与える一つの量しか持たない。たとえば、物体の質量や気体の温度はスカラー量である。これに対し「ベクトル」量は、大きさとともに方向を与えるために複数の量（成分）が必要になる。たとえば「昨夜東京では“風速 $30$ メートル”の“北西”の風が吹いた」というように、風の状況を表すためには風速と風向を表す二つの量が必要になる。物理の「力学」では物体の位置・力・速度などといった物理量がベクトル量として現れ、「電磁気学」ではベクトル量の微分が重要な役割をはたす。
　それらの詳しい話は「物理学」に任せることにして、ここではベクトルが持つ数学的な性質を学ぶ。そのため、ここで扱うベクトル量は特定の次元も単位も持たない量である。また、簡単のためにベクトルは二つの成分を持つ（二成分ベクトル）とするが、三つ以上の成分を持つベクトルの場合には、次節で学ぶ「ベクトルの外積」を除き、ここで学ぶことを単純に拡張すればよい。
　ベクトル量が大きさと方向という二つの性質を持つことから、それらを表す方法が必要になる。ベクトル量を表す方法はいくつかある。例えば、大きさ $A$ を持ちある方向を持つ量を、その文字を太字にして $A$ と表す、特殊なフォントを使い $A$ と表わす、 $A$ の上に矢印をつけて $\vec{A}$ と表すなどである。本書では点字化する時の便宜を考えて、最後の大きさを表す文字の上に矢印を添えてベクトルを表す方法を採用する。
　いくつかの成分が縦に並んだ行列を使ってベクトルを表すこともできる。たとえば、

<6-45>　(6.2.1)　 $\begin{array}{l} (\begin{matrix} 2 \\ 3 \end{matrix}) \end{array} = \vec{a}$

は一つのベクトルである[4]。このような二つの成分を持つベクトルを二成分ベクトルと呼ぶ。上式の二つの成分が $\vec{a}$ の大きさと方向にどのように関係するかは以下に説明する。また、ベクトルを行列で表す考え方では、ただ一個の成分を持つ行列の表す量が「スカラー」量であると考えてよい。
　一般にスカラー量はその大きさを表すのに、単位のスカラー量を使ってそれの何倍というように大きさを表すことができる。たとえばスカラー量 $3$ は単位スカラー量 $1$ の $3$ 倍と表すことができる。同じようにベクトル量も単位量の倍数で表すことができるが上の例でも分かるように、ベクトル量は複数の成分を持つために複数の単位量（単位ベクトル）が必要になる。スカラーとベクトルの違いは、それを一個の単位量で表すことができるか、複数の単位量を必要とするかの違いということができる。(6.2.1)式の二成分ベクトルの場合は二つの単位ベクトルが必要であるが、その二つが単位ベクトルであるためには、

二つが互いに一次独立でなければならない。すなわち、一方を使って他方を表すことができてはいけない。
単位であるためには、それぞれの大きさが $1$ でなければならない（大きさの意味はすぐにわかる）。

「二成分ベクトルに対し二つの単位ベクトルが必要」と書いたが、上の条件を満足する単位ベクトルの与え方は一つではなく一般にいくつかあり、状況に応じてどれか都合の良い一組を使うことになる。たとえば二成分ベクトルの場合、以下に単位ベクトルの代表的な選び方を二組あげておく。どちらも上の二つの条件を満たしていることを確かめるとよい（大きさに関しては後の定義が必要になる）：

<6-46>　(6.2.2)　単位ベクトル $(\vec{i}, \vec{j}) ： \begin{array}{l} \vec{i} = (\begin{matrix} 1 \\ 0 \end{matrix}), \vec{j} = (\begin{matrix} 0 \\ 1 \end{matrix}) \end{array}$

<6-47>　(6.2.3)　単位ベクトル $({\vec{e}}_{r}, {\vec{e}}_{θ}) ： \begin{array}{l} {\vec{e}}_{r} = \frac{1}{\sqrt{2}} (\begin{matrix} 1 \\ i \end{matrix}), {\vec{e}}_{θ} = \frac{1}{\sqrt{2}} (\begin{matrix} 1 \\ - i \end{matrix}) \end{array}$

(6.2.3)式の単位ベクトルを表す行列の２行目に現れる $i$ は虚数単位 $(i^{2} = - 1)$ であり、(6.2.2)式の単位ベクトルのひとつ $\vec{i}$ と混同しないよう注意せよ。
$(\vec{i}, \vec{j})$ と $({\vec{e}}_{r}, {\vec{e}}_{θ})$ を使って(6.2.1)式の二成分ベクトル $\vec{a}$ を表すことができる。その結果は

<6-48>　(6.2.4)　 $\begin{matrix} \vec{a} = \vec{i} 2 + \vec{j} 3 \\ = {\vec{e}}_{r} (\frac{2 - 3 i}{\sqrt{2}}) + {\vec{e}}_{θ} (\frac{2 + 3 i}{\sqrt{2}}) \end{matrix}$

である。 $(\vec{i}, \vec{j})$ と $({\vec{e}}_{r}, {\vec{e}}_{θ})$ に(6.2.2)式と(6.2.3)式の行列表現を直接代入して行列の掛け算と足し算の規則を使って成分をまとめると、それが確かに(6.2.1)式の $\vec{a}$ を与えていることを各自で確かめよ。

【ベクトルの図的表現】

　第三章§2で学んだように、実数と虚数の一組の数から成る複素数を平面上の一点に対応させることができ、それを利用して複素数をその「大きさ」と「偏角」を使って表すことができた。二成分ベクトルも(6.2.1)式または(6.2.4)式のように一組の数で与えられるので、複素数と同じように平面上の一点に対応させることができる。それを説明しよう。いま

<6-49>　(6.2.5)　 $\vec{a} = \vec{i} a_{1} + \vec{j} a_{2}$

のように与えられるベクトル $\vec{a}$ があったとする。この二つの成分 $(a_{1} と a_{2})$ を持つベクトル $\vec{a}$ を $(x - y)$ 平面上における $x$ 座標が $a_{1}$ で $y$ 座標が $a_{2}$ の点と原点を結ぶ直線によって表そう。直線の先端の座標 $(a_{1}, a_{2})$ がベクトルの成分であることを示すために、直線の先端に原点からその点に向かう矢印をつける。つまり原点を起点にする矢印付き直線が指す点の座標がベクトルの成分である。その様子を6.2.1図に示した。

（図6.2.1）【 $\vec{a}$ の図表現】

【（図6.2.1）の説明】
　紙面の左下で直角に交わるように水平な線分（ $x$ 軸）とそれに垂直な線分（ $y$ 軸）が描かれ、 $x$ 軸の右先端と $y$ 軸の上先端にはそれらの向きを表す矢印が付いている。直線が交わる左下の点（原点）を起点にして右上に向かう線分が描かれ、その先端にはその向きを表す矢印が付いている。その矢印の先に文字 $\vec{a}$ が記され、その線分がベクトル $\vec{a}$ を表すことを示している。 $\vec{a}$ を表す線分の先端から $x$ 軸と $y$ 軸に対して垂直に降ろされた線分が点線で描かれている。 $x$ 軸に下された点線と $x$ 軸の交点の下に文字 $a_{1}$ が記され、 $y$ 軸に下された点線と $y$ 軸の交点の左に文字 $a_{2}$ が記されている。

　　複素数と同様なベクトルの表現から、ベクトルもまた複素数と同じように円座標を用いて表すことができる。複素数ではそれを表す線分の長さを複素数の大きさとしたが、ベクトルに対しても同じように $\vec{a}$ を表す線分の長さをこのベクトルの「大きさ」とし、それを $a$ と書き、 $\vec{a}$ が $x$ 軸となす角度 $(θ)$ をこのベクトルの「偏角」とする。 $\vec{a}$ の大きさ $(a)$ と偏角 $(θ)$ を使うと、 $\vec{a}$ の二つの成分 $(a_{1} と a_{2})$ はそれぞれ

<6-50>　(6.2.6)　 $\{\begin{matrix} a_{1} = acosθ \\ a_{2} = asinθ \end{matrix}$

のように表される。あるいは逆に $(a_{1} と a_{2})$ を使って、 $a$ と $θ$ を

<6-51>　(6.2.7)　 $\{\begin{cases} a = \sqrt{a_{1}^{2} + a_{2}^{2}} \\ tan θ = \frac{a_{2}}{a_{1}} または θ = {tan}^{- 1} (\frac{a_{2}}{a_{1}}) \end{cases}$

のように表すことができる。この教科書では $\vec{a}$ の長さ（大きさ）を $\vec{a}$ の矢印記号を除いた文字で表しているが、教科書によっては $| \vec{a} |$ という表記もある。この教科書では特に断らない限り、一般にベクトルの大きさはベクトルの矢印記号を除いた文字で表すことにする。多くの教科書では「ベクトルは大きさと方向を持つ量である」とし、「ベクトルの大きさ」のことを「ベクトルの長さ」と書くこともある。それは図を使ったベクトルの表し方に由来する。方向は視覚的には矢印が向く方向とされるが、数学的には $\vec{a}$ が $x$ 軸となす角 $θ$ （偏角）を与えることによって知ることができる。

【ベクトルの加減と積】

　我々は普通の数の四則演算（足し算、引き算、掛け算、割り算）を知っている。割り算がないことを除けば、ベクトルにもこれらの演算が存在する（なぜ割り算がないかの説明は省く）。ただ、ベクトルは複数の成分を持つため、その演算規則は普通の数に対するものと少し違う。例をあげて説明しよう。
　いま二つの二成分ベクトルを

<6-52>　(6.2.8)　 $\begin{array}{l} \vec{a} = (\begin{matrix} a_{1} \\ a_{2} \end{matrix}), \begin{array}{l} \vec{b} = (\begin{matrix} b_{1} \\ b_{2} \end{matrix}) \end{array} \end{array}$

とする。これらを二成分ベクトルの単位ベクトル $(\vec{i}, \vec{j})$ を用いて表すと

<6-53>　(6.2.9)　 $\{\begin{cases} \vec{a} = \vec{i} a_{1} + \vec{j} a_{2} \\ \vec{b} = \vec{i} b_{1} + \vec{j} b_{2} \end{cases}$

である。このとき $\vec{a}$ と $\vec{b}$ の足し算（または引き算）は

<6-54>　(6.2.10)　 $\vec{a} \pm \vec{b} = \vec{i} (a_{1} \pm b_{1}) + \vec{j} (a_{2} \pm b_{2})$

と定義される。もしこれを行列形式で表すと、それは(6.2.8)式の行列を(6.1.2)式で与えた行列の足し算（引き算）の規則によって計算した結果と一致することが分かるであろう。
　ベクトルの図的な表現を使うと、二つのベクトルの加減を図を使って行う簡単な方法のあることが分かる。それを示すために $\vec{a}$ と $\vec{b}$ の足し算を具体的に実行してみる。いまベクトルを図で表すため具体的に $(a_{1}, a_{2})$ と $(b_{1}, b_{2})$ に数値を与え、

<6-55>　(6.2.11)　 $\begin{array}{l} \vec{a} = (\begin{matrix} 1 \\ 2 \end{matrix}), \begin{array}{l} \vec{b} = (\begin{matrix} 2 \\ 1 \end{matrix}) \end{array} \end{array}$

とする。 $\vec{a}$ と $\vec{b}$ の和を $\vec{c}$ とすれば、それは

<6-56>　(6.2.12)　 $\begin{array}{l} \vec{c} = \vec{a} + \vec{b} = (\begin{matrix} 3 \\ 3 \end{matrix}) \end{array}$

である。この三つのベクトルを平面上に表した図が図6.2.2である。

（図6.2.2）【ベクトル和 $\vec{c} = \vec{a} + \vec{b}$ の図表現】

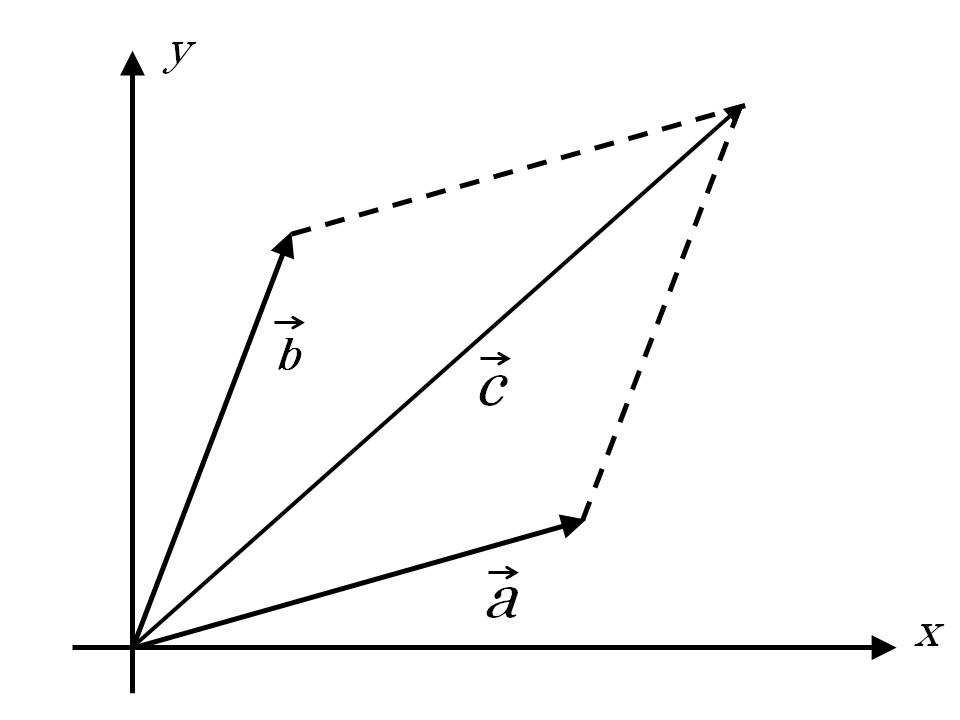
【（図6.2.2）の説明】
　紙面の左下で直角に交わるように水平な線分（ $x$ 軸）とそれに垂直な線分（ $y$ 軸）が描かれ、二本の直線の右先端と上先端にはそれらの向きを表す矢印が付いている。直線が交わる左下の点を始点にして $x$ 軸と $y$ 軸の間に斜め右上に向かう、先端に矢印が付いた三本の直線が描かれている。それらの直線のそばに上から順に $\vec{b}$ 、 $\vec{c}$ 、 $\vec{a}$ が記され、それらが対応するベクトルであることを表している。 $\vec{a}$ の先端から点線で $\vec{b}$ と同じ線分が点線で描かれており、その終点がちょうど $\vec{c}$ の先端に一致している。同様に、 $\vec{b}$ の先端から点線で $\vec{a}$ と同じ線分が $\vec{c}$ の先端まで描かれている。言いかえると、 $\vec{a}$ 、 $\vec{b}$ と二本の点線は原点を一つの頂点とする平行四辺形を作り、 $\vec{c}$ はその対角線になっている。

　上の説明にあるように $\vec{c}$ は $\vec{a}$ と $\vec{b}$ が作る平行四辺形の対角線であるから、結局 $\vec{a}$ と $\vec{b}$ を加えてできるベクトルを求めるには、 $\vec{a}$ と $\vec{b}$ を同じ始点に置いて平行四辺形を作り、その始点からの対角線を求めるとよい。これを「ベクトルの加法に対する平行四辺形則」という。
　ベクトル $\vec{a}$ に負符号がついたベクトル $(- \vec{a})$ は $\vec{a}$ と反対方向を向いたベクトル、すなわち $\vec{a}$ を表す矢印付き直線の始点と終点を交換したベクトルである。負のベクトルを使うと、 $\vec{a}$ と $\vec{b}$ の差 $(\vec{a} - \vec{b})$ は

<6-57>　(6.2.13)　 $\vec{a} - \vec{b} = \vec{a} + (- \vec{b})$

のように $\vec{a}$ と $(- \vec{b})$ のベクトル和と考え、これに対してベクトル和の規則を用いれば良い。
　ベクトルが複数の成分を持つためベクトルの積は普通の数の積と著しく異なる。最も特徴的なことは二種類の積が存在することである。一つは「内積（またはスカラー積）」とよばれる結果がスカラーになる積であり、一つは「外積（または「ベクトル積）」とよばれる結果がベクトルになる積である。

【ベクトルの内積（スカラー積）】

　二つのベクトルの「内積」は、それらの成分の積を加えた量として定義される。すなわち、(6.2.8)式または(6.2.9)式で与えたベクトル $\vec{a}$ と $\vec{b}$ の内積を $\vec{a} \cdot \vec{b}$ と書くとき、それは

<6-58>　(6.2.14)　 $\vec{a} \cdot \vec{b} = a_{1} b_{1} + a_{2} b_{2}$

である。結果が方向を持たない大きさだけの量（スカラー量）で定義されるので、「内積」を「スカラー積」ともいうのである。(6.2.2)式の単位ベクトル $\vec{i}$ と $\vec{j}$ に対して、それらの内積は、簡単な計算を行うと

<6-59>　(6.2.15)　 $\{\begin{cases} (\vec{i} \cdot \vec{i}) = (\vec{j} \cdot \vec{j}) = 1 \\ (\vec{i} \cdot \vec{j}) = (\vec{j} \cdot \vec{i}) = 0 \end{cases}$

となることがわかる。(6.2.9)式で与えた $\vec{a}$ と $\vec{b}$ の内積は(6.2.15)式を使って

<6-60>　 $\begin{array}{l} (\vec{a} \cdot \vec{b}) = (\vec{i} a_{1} + \vec{j} a_{2}) \cdot (\vec{i} b_{1} + \vec{j} b_{2}) \\ = (\vec{i} \cdot \vec{i}) a_{1} b_{1} + (\vec{i} \cdot \vec{j}) a_{1} b_{2} \\ + (\vec{j} \cdot \vec{i}) a_{2} b_{1} + (\vec{j} \cdot \vec{j}) a_{2} b_{2} \\ = a_{1} b_{1} + a_{2} b_{2} \end{array}$

と計算されたものと考えてもよい。
　(6.2.6)式でベクトルの成分をその大きさと偏角を使って表す方法を与えたが、それを使うと二つのベクトルの内積をベクトルの大きさと偏角を使って次のように表すこともできる。 $\vec{a}$ の大きさを $a$ とし、偏角を $θ_{a}$ 、 $\vec{b}$ の大きさを $b$ とし、偏角を $θ_{b}$ とすると、 $\vec{a}$ の直交座標成分 $(a_{1}, a_{2})$ と $\vec{b}$ の直交座標成分 $(b_{1}, b_{2})$ は、

<6-61>　(6.2.16)　 $\{\begin{cases} (a_{1} = a cos θ_{a}, a_{2} = a sin θ_{a}) \\ (b_{1} = b cos θ_{b}, b_{2} = b sin θ_{b}) \end{cases}$

である。
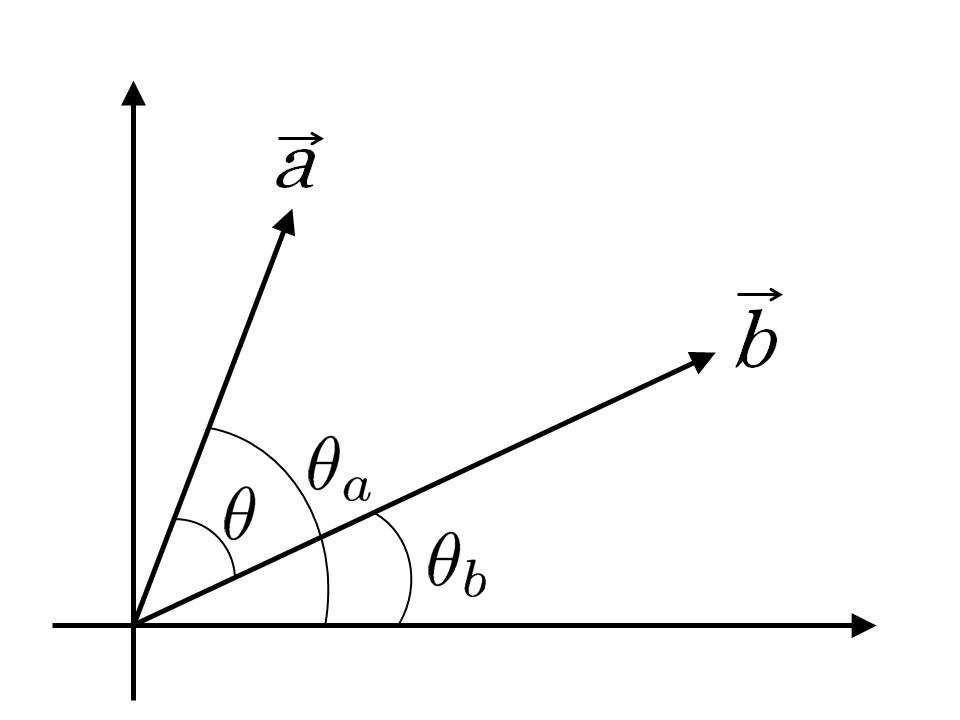
　いま便宜上 $θ_{a} \geq θ_{b}$ と考えておこう。（ $θ_{a} \leq θ_{b}$ としても結論は変わらない。）このときのベクトルの関係を6.2.3図に示した。

（図6.2.3）【 $\vec{a}$ 、 $\vec{b}$ とそれらの角度】

【（図6.2.3）の説明】
紙面の左下で直角に交わる水平な線分（ $x$ 軸）とそれに垂直な線分（ $y$ 軸）が描かれ、 $x$ 軸を表す線分の右先端には右向き矢印が、 $y$ 軸を表す線分の上先端には上向き矢印が付いている。 $x$ 軸と $y$ 軸の交点（原点）から右斜め上に向かう二本の直線が描かれており、 $y$ 軸側にある線分の先端についた矢印の先には $\vec{a}$ が、 $x$ 軸側にある線分の先端についた矢印の先には $\vec{b}$ が記されている。 $\vec{a}$ と $\vec{b}$ の間、 $\vec{a}$ と $x$ 軸の間、 $\vec{b}$ と $x$ 軸の間には、それらがなす角を表す小さな円弧が原点を中心にして描かれており、その横に角度の大きさを表す文字が順に $θ_{a}$ 、 $θ_{b}$ 、 $θ$ と記されている。

　このとき二つのベクトルの内積(6.2.14)式を(6.2.16)式に与えられるベクトルの大きさとそれらが $x$ 軸と作る角度を使って

<6-62>　(6.2.17)　 $\begin{array}{l} \vec{a} \cdot \vec{b} = a b (cos θ_{a} cos θ_{b} + sin θ_{a} sin θ_{b}) \\ = a b cos (θ_{a} - θ_{b}) \\ = a b cos θ \end{array}$

と書くことができる。途中で角度 $θ_{1}$ と $θ_{2}$ に関する三角関数の加法定理

<6-63>　(6.2.18)　 $\begin{array}{l} cos (θ_{1} \pm θ_{2}) = cos θ_{1} cos θ_{2} \\ \mp sin θ_{1} sin θ_{2} \end{array}$

を用い、さらに $\vec{a}$ と $\vec{b}$ がなす角の差 $(θ_{a} - θ_{b})$ を $θ$ を使って書いた。ベクトルの内積に関する(6.2.17)式はしばしば次のように表現される。

\vec{a}

\vec{b}

(\vec{a} \cdot \vec{b})

\vec{a}

\vec{b}

(a b)

(cos θ)

「

\vec{a}

と

\vec{b}

がなす角

θ

」が、二つのベクトルがなす内側の狭い方の角か、それとも外側の広い方の角かと迷う人はいないであろうが、もし迷うことがあれば

「 180^{\circ} (= π ラジアン) より小さいほうの角（狭角）」

である。
　二つのベクトルの内積を与える(6.2.17)式を

<6-64>　(6.2.19)　 $\vec{a} \cdot \vec{b} = a (b cos θ) = b (a cos θ)$

と書いたときの右辺にあるカッコの意味、たとえば $(a cos θ)$ を考える。その様子を図6.2.4に描いたので、それを参照せよ。

（図6.2.4）【ベクトルの内積と射影】

【（図6.2.4）の説明】
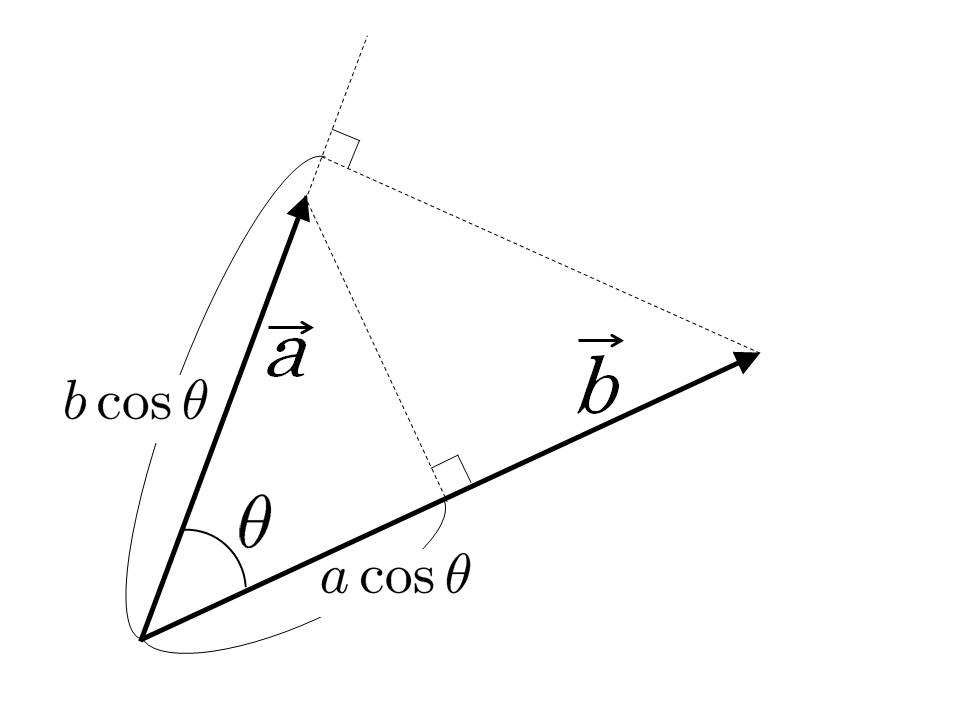
紙面左下の一点から二本の矢印付き線分が右斜め上の異なる方向に向かって描かれており、二つの線分が作る角度を表す小さな円弧が始点を中心に描かれ、その横に角度の大きさを表す文字

θ

が記されている。上側の矢印付き線分のすぐ下にはそれがベクトルであることを表す

\vec{a}

が記され、下側の矢印付き線分のすぐ上には文字

\vec{b}

が記されている。図では、

\vec{a}

の長さは

\vec{b}

の長さより短く描かれている。

\vec{a}

の先端から

\vec{b}

に向かって垂直に点線が引かれ、それと

\vec{b}

との交点に点線が垂線であることを表す記号

□

がつけられている。その点と、

\vec{a}

と、

\vec{b}

の始点の間にその長さを表す文字

a cos θ

が記されている。同様に、

\vec{b}

の先端から

\vec{a}

を延長して描かれた点線上に垂直な点線が引かれ、それと

\vec{a}

の延長線との交点の間に点線が垂線であることを表す記号

□

がついている。また、その点と、

\vec{a}

と

\vec{b}

の始点の間にその長さを表す文字

b cos θ

が記されている。

　 $\vec{a}$ の先端から $\vec{b}$ 方向に延長した直線に向かって降ろした垂直な直線（垂線）が $\vec{b}$ 方向の延長直線と交わる点をその垂線の“足”と言う。そして、両ベクトルの始点からその足までの長さ $(a cos θ)$ を「 $\vec{a}$ の $\vec{b}$ 方向射影」という。同様に、 $(b cos θ)$ は「 $\vec{b}$ の $\vec{a}$ 方向射影」である。したがって(6.2.19)式を

(\vec{a} \cdot \vec{b})

\vec{a}

\vec{b}

\vec{a}

\vec{b}

\vec{a}

\vec{b}

と表現することもできる。
　内積に現われる角に対して(6.2.18)式の下で与えた定義「二つのベクトルのなす角は

180^{\circ} (= π ラジアン)

より小さいほうの角」から、

0 \leq θ \leq π

なので、

cos θ

は

- 1 \leq cos θ \leq 1

の値を持つ。したがって、もし二つのベクトルが同じ方向を向いていれば

θ = 0

であるから

cos θ = 1

である。したがって

\vec{a}

と

\vec{b}

の内積はそれらの大きさの積

(a b)

になり、二つのベクトルの内積が作れる最大の大きさを与える。もし二つのベクトルが互いに垂直な方向を向いていれば

θ = \frac{π}{2}

であるから

cos θ = 0

である。このとき、

(\vec{a} \cdot \vec{b})

は最小値の

0

になる。すなわち、

0

さらに、もし二つのベクトルが反対方向を向いていれば

θ = π

であるから

cos θ = - 1

である。したがって

(\vec{a} \cdot \vec{b})

は

(- a b)

になり、二つのベクトルの内積が持ち得る最小の大きさを与える。
　たとえば、(6.2.2)式で与えられた単位ベクトル

\vec{i}

と

\vec{j}

の内積は、それらが直交しているので

0

であり、同じ単位ベクトル同士の内積は、それらが同じ方向を向いているので

1

である。これは(6.2.15)式で単位ベクトルに与えた内積の関係式と一致する。また、この逆も成り立ち、

0

0

　特別な場合として

\vec{a}

どうしの内積がある。この時は内積を作るベクトルのなす角は

0

であるから、

(\vec{a} \cdot \vec{a}) = a^{2}

となる。したがってベクトル

\vec{a}

の大きさを、そのベクトルどうしの内積によって、

<6-65>　(6.2.20)　 $a = \sqrt{\vec{a} \cdot \vec{a}}$

と与えられる。ベクトルの大きさを表すときに、この表現は非常に多く使われる。

【ベクトルの外積（ベクトル積）】

　もう一つのベクトル同士の積である「外積（ベクトル積）」は大学で初めて学ぶ概念であるために、最初はむずかしく感じるであろう。しかし「外積」は物理学にとって欠かせない非常に重要な量であり、これを理解しなければ物理学の最も肝心な部分を理解することが出来ない。しっかりと学習してほしい。
　内積がベクトルの方向射影を使った二つの積という、ベクトルが作る面内の概念であるのに対して、外積はその面に垂直な方向を含む空間的な概念である。これが重要な意味を持つ典型的な例は天体の運動である。例えば、地球は太陽の周りを約365日で一回転し、毎年ほぼ同じ面内のほぼ同じ場所に戻って来る。もし宇宙のどこかに地球人以外の知的生命体が存在したとして、我々が彼等と友好的な関係を築こうと彼等に対し我々が住む地球の運行についていろいろと情報を送りたかったとする。そのときには彼等に二つの情報を伝えれば十分である。「我々の地球は一年で一回太陽の周りをまわる」ことと「地球の軌道はいつも同じ面内にある」ことである。もし彼等が地球人と同じ程度の知能を持っていたら、我々が万有引力の法則の下に生きている生命体であることを含め、この二つの情報だけで相当のことが分かるはずである。この二つの情報をまとめて簡単に与えるのが「角運動量」という二つのベクトルで作られる外積である。

【余談】
「約 $365$ 日で地球は面内の同じ場所に戻って来る。」と書いたが、実はほんの少し違った場所に戻ってくる。その場所は約 $10$ 万年くらいかけて軌道面（公転面）に対しゆっくりと上下に動く。この出来事にも「角運動量」が密接に関係している。 $10$ 万年という周期は地球に氷河期が訪れる周期と大体同じであるが、その因果関係は分からない。

　外積は二つのベクトルを使って作られる。そのベクトルを $\vec{a}$ と $\vec{b}$ とする。その様子を図6.2.5に描いてある。

（図6.2.5）【ベクトルの外積】

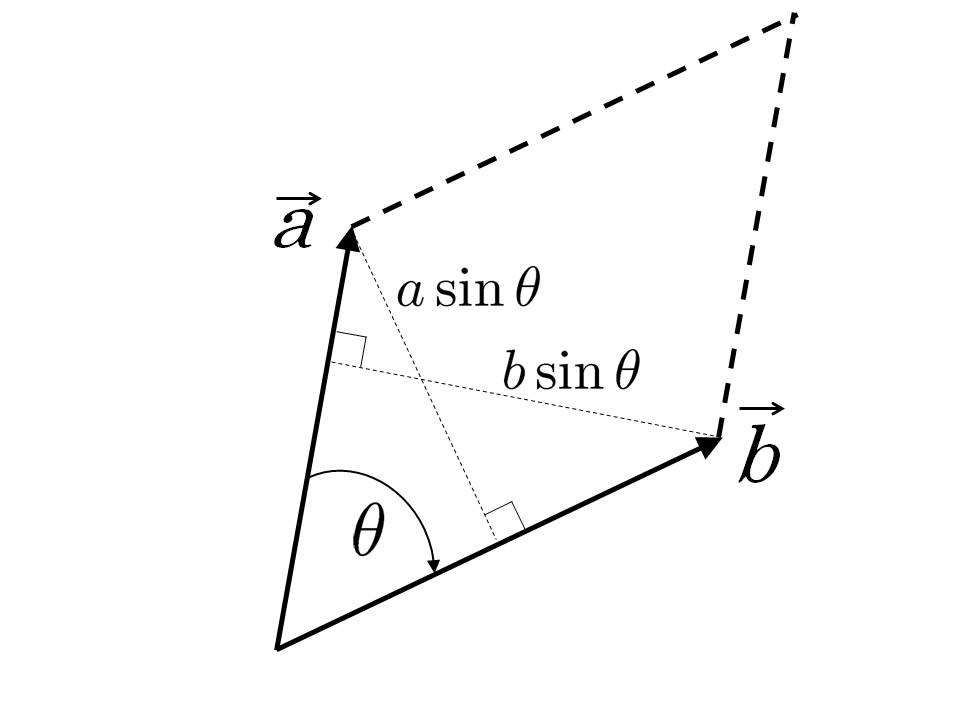
【（図6.2.5）の説明】
　紙面左下の一点から右斜め上の異なる方向に向かって二本の矢印付き線分が描かれており、二本の線分の始点を中心に線分間の角度を表す小さな円弧が描かれ、下方の線分と交わる円弧の先端に小さな矢印が描かれている。矢印は円弧に沿って時計回りする回転の向きを示す。円弧の内側にその角度を表す文字 $θ$ が記されている。上側に描かれた矢印付き線分の先端左にはそれがベクトルであることを表す $\vec{a}$ が記され、下側にある矢印付き線分の先端右には文字 $\vec{b}$ が記されている。 $\vec{a}$ の先端から $\vec{b}$ に点線で描かれた垂線が降ろされ、それと $\vec{b}$ との交点に点線が垂線であることを示す記号 $□$ がつけられている。点線の右側にはその点線が表す線分の長さを表す文字 $a sin θ$ が記されている。同様に、 $\vec{b}$ の先端から $\vec{a}$ に点線で描かれた垂線が降ろされ、それと $\vec{a}$ の交点に点線が垂線であることを示す記号 $□$ がつけられている。点線の上部にはその点線の長さを表す文字 $b sin θ$ が記されている。さらに、 $\vec{a}$ の先端から $\vec{b}$ に平行な、 $\vec{b}$ と同じ長さで破線が描かれ、 $\vec{b}$ の先端から $\vec{a}$ に平行な、 $\vec{a}$ と同じ長さの破線が描かれている。二つの破線は紙面右上部の一点で交わる。結局、 $\vec{a}$ と $\vec{b}$ と二本の破線は一つの平行四辺形を形成している。

　 $\vec{a}$ と $\vec{b}$ の外積を $\vec{a} \times \vec{b}$ と書く。外積の最も重要な特徴はスカラー量である内積と違って、それがベクトルであるということである。したがって外積は大きさと同時に方向を持つ。その方向は外積の書き方によって決まり、その規則はしばしば「右手の規則」または「右ネジの規則」と呼ばれる。すなわち、右手の三本の指（親指、人差し指、中指）を互いに直角に開いて三本の指のつけ根を二つのベクトルの始点に対応させ、親指を $\vec{a}$ 、人差し指を $\vec{b}$ に対応させたとき、親指と人差し指に垂直な中指の方向が $\vec{a} \times \vec{b}$ の方向である。別な言い方をすると、外積の式の前に置かれたベクトル（今の場合は $\vec{a}$ ）から後に置かれたたベクトル（今の場合は $\vec{b}$ ）に向かって右ネジを回した時、ネジの進む方向が $\vec{a} \times \vec{b}$ の方向であると言っても同じである。
　外積の大きさは、二つのベクトルのなす角を $θ$ とすれば $a b sin θ$ で与えられる。この大きさは簡単な幾何学的意味を持っている。 $(a sin θ)$ が $\vec{a}$ から $\vec{b}$ に降ろした垂線の長さであると同時に平行四辺形の一つの高さであり、 $(b sin θ)$ が $\vec{b}$ から $\vec{a}$ に降ろした垂線の長さであると同時に平行四辺形のもう一つの高さであることに気がつけば、外積の大きさ $ab sin θ = (a sin θ) \times b = (b sin θ) \times a$ は二つのベクトルで作られる平行四辺形の面積になっていることに気がつくであろう。つまり、

\vec{a} \times \vec{b}

\vec{a}

\vec{b}

2

【ベクトルの回転と回転行列】

　二つの成分を持つベクトルを $(x - y)$ 座標面上にある矢印がついた線分で表すことが出来ることを知った。そのとき線分の矢印のない端を $(x - y)$ 座標面の原点に置いたとき、矢印がついた端の $x$ 座標と $y$ 座標がベクトルの二つの成分を与える。(6.2.2)式で導入した二つの単位ベクトル $\vec{i}$ と $\vec{j}$ をそのように $(x - y)$ 面上で表せば、それぞれは $x$ 軸と $y$ 軸上にある大きさ（長さ） $1$ のベクトルである。また、そうであるからこそ、 $\vec{a}$ が

<6-66>　(6.2.21)　 $\vec{a} = \vec{i} a_{1} + \vec{j} a_{2}$

と表されるのである。二つの単位ベクトルに対し、それらの内積を与えた(6.2.15)式をもう一度書くと、

<6-67>　(6.2.22)　 $\{\begin{cases} (\vec{i} \cdot \vec{i}) = (\vec{j} \cdot \vec{j}) = 1 \\ (\vec{i} \cdot \vec{j}) = (\vec{j} \cdot \vec{i}) = 0 \end{cases}$

であった。さらに(6.2.8)式の二つのベクトル $\vec{a}$ と $\vec{b}$ を $(\vec{i}, \vec{j})$ を使って表した(6.2.9)式をもう一度与えると

<6-68>　(6.2.23)　 $\{\begin{cases} \vec{a} = \vec{i} a_{1} + \vec{j} a_{2} \\ \vec{b} = \vec{i} b_{1} + \vec{j} b_{2} \end{cases}$

である。(6.2.22)式に注意しながらこれらの内積を計算すると

<6-69>　(6.2.24)　 $\begin{array}{l} \vec{a} \cdot \vec{b} = (\vec{i} a_{1} + \vec{j} a_{2}) \cdot (\vec{i} b_{1} + \vec{j} b_{2}) \\ = a_{1} b_{1} + a_{2} b_{2} \end{array}$

で、結果は(6.2.14)式と一致する。平面にあるどのようなベクトルも単位ベクトル $(\vec{i}, \vec{j})$ を使って(6.2.23)式のように表すことができ、(6.2.22)式に注意しながらそれらの内積を機械的に計算すれば、必ず正しい結果を得ることができる。
　 $(x - y)$ 面にある一つの点の座標を $(x, y)$ とし、座標原点からその点に向かうベクトルを $\vec{r}$ とする。このベクトルを単位ベクトル $\vec{i}$ と $\vec{j}$ を使って表すと、

<6-70>　(6.2.25)　 $\vec{r} = \vec{i} x + \vec{j} y$

であることはこれまでの知識から理解できるであろう。このように平面内にある点の位置を表すベクトルを「位置ベクトル」という。
　 $(x - y)$ 平面上のベクトルが長さを変えずにその角度を $θ$ だけ変えることがある。これをベクトルの回転と呼ぶ。今、座標 $(x, y)$ を表す位置ベクトルが紙面上に描かれているとして、それを原点を中心として左回りに（ $x$ 軸からの角度が増える向きに） $θ$ 回転した。回転した後の位置ベクトルが表す座標点を $(x', y')$ とする。 $\vec{r}$ を $θ$ 回転して $\vec{i} x' + \vec{j} y' \equiv \vec{r}'$ に移すと言っても良い。このとき、 $(x', y')$ を $(x, y)$ と $θ$ を使って次のように表すことができる。

<6-71>　(6.2.26)　 $\{\begin{cases} x^{'} = x cos θ - y sin θ \\ y^{'} = x sin θ + y cos θ \end{cases}$

【証明】
$\vec{r} = \vec{i} x + \vec{j} y$ の大きさを $r$ とすれば、 $(\vec{r} \cdot \vec{r}) = x^{2} + y^{2}$ なので、 $r = \sqrt{(\vec{r} \cdot \vec{r})} = \sqrt{x^{2} + y^{2}}$ である。また、 $\vec{r}$ と $x$ 軸のなす角を $θ_{0}$ とすれば、
<6-72>　 $(a) \{\begin{cases} x = r cos θ_{0} \\ y = r sin θ_{0} \end{cases}$
である。 $\vec{r}'$ は $x$ 軸と角 $θ_{0}$ をなす $\vec{r}$ から角度が増える方向にさらに $θ$ 回転したベクトルであるので、それが $x$ 軸となす角度は $(θ_{0} + θ)$ となる。回転で $\vec{r}'$ の長さ（大きさ）は $\vec{r}$ と変わらず同じ $r$ なので、したがって $\vec{r}'$ の成分 $(x', y')$ は
<6-73>　 $(b) \{\begin{cases} x' = r cos (θ_{0} + θ) \\ = r (cos θ_{0} cos θ - sin θ_{0} sin θ) \\ = x cos θ - y sin θ \\ y' = r sin (θ_{0} + θ) \\ = r (sin θ_{0} cos θ + cos θ_{0} sin θ) \\ = y cos θ + x sin θ \end{cases}$
となり、(6.2.26)式が得られる。ここで、最後の式を得るのに三角関数の加法定理
<6-74>　 $(c) \{\begin{cases} sin (a \pm b) = sin a cos b \pm cos a sin b \\ cos (a \pm b) = cos a cos b \mp sin a sin b \end{cases}$
と $(a)$ 式を用いた。

(6.1.4)式で与えた行列の掛け算のルールにしたがい行列を使って(6.2.26)式を

<6-75>　(6.2.27)　 $\begin{array}{l} (\begin{matrix} x' \\ y' \end{matrix}) = \begin{array}{l} (\begin{matrix} cos θ & - sin θ \\ sin θ & cos θ \end{matrix}) \begin{array}{l} (\begin{matrix} x \\ y \end{matrix}) \end{array} \end{array} \end{array}$

のように書くことができる。右辺にあり、座標点 $(x, y)$ を角 $θ$ だけ回転して別な点 $(x^{'}, y^{'})$ に移す働きをする行列

<6-76>　(6.2.28)　 $R (θ) = \begin{array}{l} (\begin{matrix} cos θ & - sin θ \\ sin θ & cos θ \end{matrix}) \end{array}$

を「回転行列」という。回転前のベクトルと回転後のベクトルの様子を6.2.6図に示す。

（図6.2.6）【ベクトルの回転】

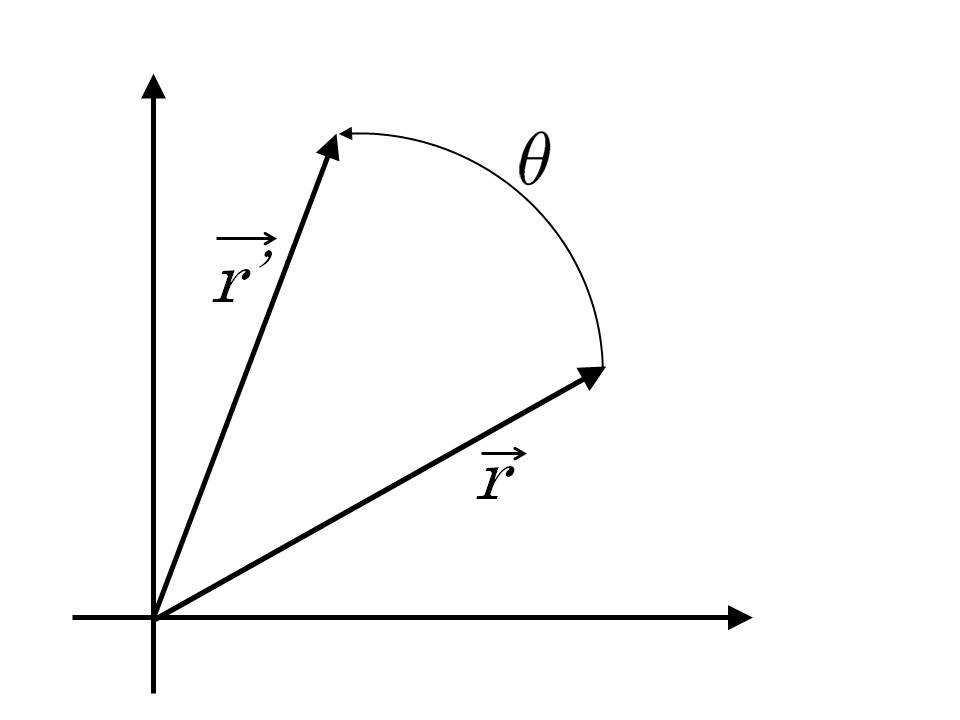
【（図6.2.6）の説明】
　紙面下方に水平な線分（ $x$ 軸）と、それと紙面左下で直角に交わる線分（ $y$ 軸）が描かれている。水平な線分の右端と、それに直交する線分の上端にはそれぞれ正の向きを表す矢印がついている。線分の交点から右斜め上方に矢印が付いた同じ長さの線分が二本、小さな角度をなして描かれている。 $x$ 軸に近い線分下側に文字 $\vec{r}$ が付され、 $y$ 軸に近い線分上側に文字 $\vec{r}'$ が付されている。交点を中心に、線分の長さを半径として線分の先端をつなぐ円弧が描かれており、円弧のそばには二つの線分がなす角度を表す文字 $θ$ が記されている。

　回転行列は面白い性質を持っている。そのうちのいくつかを証明なしにあげておく。

【回転行列の性質】

行列 $R (θ)$ に対する行列式を $det [R (θ)]$ と書けば、 $det [R (θ)] = 1$ である。
行列 $R (θ)$ の逆行列を $R^{- 1} (θ)$ と書けば、 $R^{- 1} (θ) = R (- θ)$ である。
$R (θ)$ で関係づけられる二つのベクトルの大きさは変わらない。たとえば(6.2.27)式では $\sqrt{{x'}^{2} + {y'}^{2}} = \sqrt{x^{2} + y^{2}}$ である。

上の性質を持つ行列を数学では「ユニタリー行列」という。物理ではこのユニタリー行列がいろいろな所に現れ、とても重要な役割を果たすのであるが、ここではこれ以上立ち入らない。

【余談】
ユニタリー行列は数学の「群論」と密接に関係している。「群論」が「量子力学」で非常に重要な役割を演じていることが理解された $1940$ 年代、多くの物理学者が「群論」の勉強に熱中し、その狂熱的な流行はまたたく間に世界中に広まった。それがまるで伝染病のペストのような勢いであったというので、物理学者の間でその現象は「グルッペン・ペスト」と呼ばれた。この逸話は物理学で扱う自然現象と行列が持つ性質の間に密接な関係があることを表している。実際にそれが意味したことは実に驚くべきものであった。その一端は本シリーズの別冊「現代の物理学」に紹介されているので、興味があれば読むと良い。

　(6.2.27)式の回転は二つの量 $(x, y)$ をそれらが一次で組み合わされた量 $(x', y')$ に変える。このような操作を「一次変換（または線型変換）」という[5]。すなわち、回転は一次変換の一つである。他にも重要な一次変換がたくさんあるが、ここでは一次変換の最も重要な性質を回転を例にして一つだけ述べておく。
　今、二つの回転を引き続き行うことを考える。すなわち、ベクトル $\vec{r} = \vec{i} x + \vec{j} y$ に角度 $θ_{1}$ の回転を行って出来たベクトルを $\vec{r}' = \vec{i} x' + \vec{j} y'$ とし、それに引き続き角度 $θ_{2}$ の回転を行う。それを行列を使って表して見よう。最初の回転で $\vec{r}$ は(6.2.27)式から

<6-77>　(6.2.29)　 $\begin{array}{l} (\begin{matrix} x \\ y \end{matrix}) \end{array} \to (\begin{array}{l} x' \\ y' \end{array}) = R (θ_{1}) (\begin{array}{l} x \\ y \end{array})$

である。同様に、引き続く回転で $\vec{r}'$ は

<6-78>　(6.2.30)　 $\begin{array}{l} (\begin{array}{l} x' \\ y' \end{array}) \to (\begin{array}{l} x " \\ y " \end{array}) = R (θ_{2}) (\begin{array}{l} x' \\ y' \end{array}) \\ = R (θ_{2}) R (θ_{1}) (\begin{array}{l} x \\ y \end{array}) \end{array}$

となるが、 $\vec{r}$ に対して角度 $θ_{1}$ の回転を行い、その後に角度 $θ_{2}$ の回転を行うのであるから、結局この引き続く二度の回転で作られる位置ベクトル ${\vec{r}}^{"} = \vec{i} x " + \vec{j} y "$ は $\vec{r}$ に対して角度 $(θ_{1} + θ_{2})$ の回転を行なった結果と同等でなければならない。したがって(6.2.30)式に現れる回転行列の積は $R (θ_{2}) R (θ_{1}) = R (θ_{1} + θ_{2})$ でなければならない。この式の左辺を具体的に書けば

<6-79>　(6.2.31)　 $\begin{array}{l} R (θ_{2}) R (θ_{1}) = (\begin{array}{c} cos θ_{2} & - sin θ_{2} \\ sin θ_{2} & cos θ_{2} \end{array}) \\ \times (\begin{array}{c} cos θ_{1} & - sin θ_{1} \\ sin θ_{1} & cos θ_{1} \end{array}) \end{array}$

である。これを(6.1.4)式に与えた行列の掛け算の規則にしたがって計算すれば

<6-80>　(6.2.32)　 $\begin{array}{l} R (θ_{2}) R (θ_{1}) \\ = (\begin{array}{c} (cos θ_{1} cos θ_{2} - sin θ_{1} sin θ_{2}) & (- sin θ_{1} cos θ_{2} - cos θ_{1} sin θ_{2}) \\ (cos θ_{1} sin θ_{2} + sin θ_{1} cos θ_{2}) & (- sin θ_{1} sin θ_{2} + cos θ_{1} cos θ_{2}) \end{array}) \end{array}$

である。一方 $R (θ_{1} + θ_{2})$ は

<6-81>　(6.2.33)　 $\begin{array}{l} R (θ_{1} + θ_{2}) \\ = (\begin{array}{c} cos (θ_{1} + θ_{2}) & - sin (θ_{1} + θ_{2}) \\ sin (θ_{1} + θ_{2}) & cos (θ_{1} + θ_{2}) \end{array}) \end{array}$

であり、これが(6.3.32)式に等しくなければならない。すでに気がついたと思うが、この結果は少し前に用いた三角関数の加法定理を与える。すなわち、 $R (θ_{2}) R (θ_{1}) = R (θ_{1} + θ_{2})$ が確かに成り立っている。実は「三角関数の加法定理には元々この回転の数学がその背景にある」というのが正しいのである。

【ベクトルの微分：ナブラ演算子と勾配（グラディエント）】

　物理で現れるベクトルに、その成分が座標や時間の関数であるベクトルがある。そのようなベクトルは位置や時間が異なれば、大きさも方向も変わる。ということは、ベクトル座標や時間に関する微分が存在することにもなる。実際に「電磁気学」にはそのような物理量が多数存在し、大学における「電磁気学」の学習はさながらそのようなベクトルの微分計算との戦いでもある。しかしながら、その戦いの見返りは大きい。近代社会の土台になった「相対性理論」も「量子力学」もその戦果なのである。
　力学で実際に現れる物理量を使ってベクトル量の微分を説明しよう。前節で $(x - y)$ 平面上にある物体の位置を指定するために二つの成分 $(x と y)$ を持つ位置ベクトルを導入した。もしこの成分 $(x 座標と t 座標)$ が時間 $t$ とともに変わるとすれば、ベクトルの大きさや方向も $t$ とともに変わることになる。実際に、時間とともに変わる成分を持つ位置ベクトルを

<6-82>　(6.2.34)　 $\vec{r} (t) = \vec{i} x (t) + \vec{j} y (t)$

とすれば、(6.2.7)式より $\vec{r} (t)$ の大きさ $\sqrt{{x (t)}^{2} + {y (t)}^{2}}$ は時間とともに変わり、 $\vec{r} (t)$ の方向を表す $x$ 軸からの角度（偏角） ${tan}^{- 1} (\frac{y (t)}{x (t)})$ もやはり時間とともに変わる。「第二章§4. 運動と微分の関係」で、未来の時刻における物体の位置を予言するためには、時間に関する位置の導関数を知れば良いことを知った。ここでも同じで、任意の時刻 $t$ における $x (t)$ や $y (t)$ を知るためにはそれらの時間に関する導関数 $(\frac{dx}{dt}, \frac{dy}{dt}) = (\dot{x}, \dot{y})$ を知ればよい。ここで時間の関数（たとえば $A (t)$ ）の上についている $(\cdot)$ 記号（たとえば $\dot{A}$ ）は時間微分を表す「ニュートンの記法」 $(\dot{A} (t) \equiv \frac{dA}{dt})$ である。もし $(\dot{x}, \dot{y})$ が分かったとする。そうすると、それらを成分に持つベクトルを考えることが出来る。一般に、その成分もまた $t$ の関数であるから、それらを成分に持つベクトルを

<6-83>　(6.2.35)　 $\vec{v} (t) \equiv \vec{i} \frac{dx (t)}{dt} + \vec{j} \frac{dy (t)}{dt}$

と書くことができる。このベクトル $\vec{v} (t)$ を物理では「速度」と呼ぶ。速度が位置ベクトルの時間微分であることを明らかにするために、これを

<6-84>　(6.2.36)　 $\vec{v} (t) = \frac{d \vec{r} (t)}{dt}$

と書くことも多い。さらに、(6.2.35)式の成分を $\frac{dx (t)}{dt} \equiv v_{x} (t)$ 、 $\frac{dy (t)}{dt} \equiv v_{y} (t)$ と書けば、

<6-85>　(6.2.37)　 $\vec{v} (t) = \vec{i} v_{x} (t) + \vec{j} v_{y} (t)$

である。 $\vec{v} (t)$ の大きさを、ベクトルを表す矢印を取り除いて $v (t)$ と書き、成分を使って表せば

<6-86>　(6.2.38)　 $v (t) = \sqrt{v_{x} (t)^{2} + v_{y} (t)^{2}}$

である。物理ではこの速度の大きさ（スカラー量）を「速さ」と呼んで、方向を持つベクトル量の「速度」とは厳密に区別する。
　速度ベクトルと同様に「加速度ベクトル」を考えることもできる。それを $\vec{a} (t)$ とすれば

<6-87>　(6.2.39)　 $\vec{a} (t) = \frac{d \vec{v} (t)}{dt} = \frac{d^{2} \vec{r} (t)}{d t^{2}}$

である。 $\vec{a} (t)$ を成分を使って

<6-88>　(6.2.40)　 $\vec{a} (t) = \vec{i} a_{x} (t) + \vec{j} a_{y} (t)$

と表すこともできる。
　(6.2.39)式が示すように、加速度ベクトルは時間の関数である速度ベクトルを時間で微分して得られる。そのことから生まれやすい思い違いがある。そのことを注意しておく。それは速度の大きさ（速さ）と加速度の大きさの関係である。すなわち、加速度の大きさは成分を使うと <6-89> $(a (t) = \sqrt{a_{x} (t)^{2} + a_{y} (t)^{2}})$ であり、速度ベクトルの大きさ（速さ）は <6-90> $(v (t) = \sqrt{v_{x} (t)^{2} + v_{y} (t)^{2}})$ である。加速度ベクトルと速度ベクトルの関係が <6-91> $(\vec{a} (t) = \frac{d \vec{v} (t)}{dt})$ であるからといって、加速度の大きさは速さの微分ではない <6-92> $(a (t) \neq \frac{dv (t)}{dt})$ 。詳しい証明は「物理学」で行うが、これを理解することはとても重要である。たとえば、台風が北半球では左回りの渦を巻き、南半球では右回りになる理由にはこのことが大いに関係している。
　物理学では、運動する物体がいつどこに到達するかに興味がある場合もあれば、注目する物理量がいつどこにどれだけあるかに興味がある場合もある。前者は台風の進路に興味を持つのと似ており、後者は自分が住む地域の雨量に興味を持つのと似ている。あるいは、前者は行楽地に向かう自動車が今どこを走っているかを知るのと似ており、後者はこの先のサービスエリアにある駐車場の混み具合を知るのと似ている。
　後者の状況、すなわち、時刻 $t$ で点 $(x, y)$ における物理量 $A$ （たとえば、特定のサービスエリアの駐車場における自動車の台数）を考える。強調すべきは、今の場合 $(x, y)$ は $A$ を測定する位置の座標であるから、時刻が変わってもその点の座標が変わることはない。しかし、 $A$ の値はそれをどこで測るかによっても変わるし、いつ測るかによっても変わる。すなわち $A$ は $\vec{r}$ と $t$ の関数であるので、 $A (\vec{r}, t)$ と書くことができる。もちろん、ここで

<6-93>　(6.2.41)　 $\vec{r} = \vec{i} x + \vec{j} y$

である。もう一度断っておくが、 $x$ と $y$ は平面上の一点を指定する値であって、 $t$ によって変わらない。
　ある位置で $A (\vec{r}, t)$ が与えられたとき、異なる位置における $A$ を知りたいとする。微分の章で学んだように、 $A$ は二つの変数 $x$ と $y$ を持つので、他の位置の情報から点 $\vec{r}$ における $A$ を予言するためには二つの微分係数 $\frac{\partial A}{\partial x}$ と $\frac{\partial A}{\partial y}$ が必要になる。そこで、この二つの量を成分に持つベクトルを作り、それを

<6-94>　(6.2.42)　 $\begin{array}{l} \vec{i} \frac{\partial A}{\partial x} + \vec{j} \frac{\partial A}{\partial y} = (\vec{i} \frac{\partial}{\partial x} + \vec{j} \frac{\partial}{\partial y}) A (\vec{r}, t) \\ \equiv \nabla A または grad A \end{array}$

と書く。 $A$ の偏微分係数を成分に持つこのベクトル $\nabla A$ には「 $A$ の勾配（グラディエント）」という名前がついていて、「グラディエント $A$ 」または「ナブラ $A$ 」と読まれる。 $\nabla A$ はベクトル量であるから、それが分かるということは、その成分である $\frac{\partial A}{\partial x}$ と $\frac{\partial A}{\partial y}$ が分かるということである。
　記号 $\nabla$ （ナブラ）は

<6-95>　(6.2.43)　 $\nabla = \vec{i} \frac{\partial}{\partial x} + \vec{j} \frac{\partial}{\partial y}$

であり、「第二章§1. 導関数（微分係数）」の節で説明した、読者にある種の演算を命じる演算子の一つである。すなわち $\nabla$ は読者に「その右側にある関数の $x$ と $y$ による偏微分係数を成分に持ったベクトルを作る演算を行なえ」と命じる。ただ、これまでの演算子と違うのは、「 $\nabla$ は二つの偏微分係数を成分とするベクトル」であることである。ここでは $\vec{r}$ が二つの成分を持つ(6.2.41)式の場合を考えているので $\nabla$ もまた対応する二つの変数の偏微分係数から成るが、もし位置ベクトルが三つの成分を持てば $\nabla$ も対応する三つの変数の偏微分係数を含む。位置ベクトルが三つの成分を持つ場合は次節で扱われる。
　物事を必要以上に複雑にしていると感じるかもしれないが、以前にも書いたように、一つのことで得た概念を抽象化して拡張し、適用範囲を拡げることは自然科学の常套手段であり、その歴史が私たちの社会の発展に多くの実りをもたらして来た。この場合も理解への苦労に価する見返りがある。実際に、この節と次節で学ぶ微分に関連する考え方は、今や分野を越えて「経済学」や「政治学」の世界でも広く使われている。

【ベクトルの微分：発散（ダイバージェンス）】

　前節では $(x - y)$ 面内の一点にある一つの量 $A (\vec{r})$ を考えたが、場合によっては面内の一点における重要な情報を表すのに二つの量が必要なこともある。たとえば、秋になると日本には多くの台風がやってくる。気象庁は台風の進路を予想して、その情報を時々刻々我々に知らせてくれる。台風情報には「中心部の気圧」と台風が「進む方向」が必要であり、気象庁はそれを地図上で気圧を示す数値と予想進路を示す矢印を使って我々に与えてくれる。これは地点 $\vec{r}$ における気圧を大きさとし、進路を方向とする一つのベクトルである。このベクトルを $\vec{T} (\vec{r})$ 、その大きさ（気圧）を $T (\vec{r})$ 、 $\vec{T}$ の方向（台風の進路）と $x$ 軸のなす角を $θ$ とすれば、 $\vec{T} (\vec{r})$ の $x$ 成分 $(T_{x} (\vec{r}))$ と $y$ 成分 $(T_{y} (\vec{r}))$ は、

<6-96>　(6.2.44)　 $\{\begin{cases} T_{x} (\vec{r}) = T (\vec{r}) cos θ \\ T_{y} (\vec{r}) = T (\vec{r}) sin θ \end{cases}$

である。この成分と、 $x$ 方向の単位ベクトル $\vec{i}$ と $y$ 方向の単位ベクトル $\vec{j}$ を使って $\vec{T} (\vec{r})$ を

<6-97>　(6.2.45)　 $\vec{T} (\vec{r}) = \vec{i} T_{x} (\vec{r}) + \vec{j} T_{y} (\vec{r})$

と表すことができる。 $\vec{T} (\vec{r})$ の二つの成分 $(T_{x}, T_{y})$ が観測地点を表す $\vec{r}$ に依存していることをもう一度強調しておく。また、 $T_{x}$ および $T_{y}$ の添え字 $x$ と $y$ は「 $\vec{T}$ の $x$ 軸に沿った成分と $y$ 軸に沿った成分」という意味であり、座標 $\vec{r}$ の $x$ 成分 $(x)$ および $y$ 成分 $(y)$ とは関係のないことを十分に理解してほしい。
　具体例はあげないが、物理ではこのようなベクトルが非常に多く現れる。その代表として上の $\vec{T} (\vec{r})$ をしばらく使うことにする。ある点 $\vec{r}$ における $\vec{T}$ の知識をもとにして、そこから少し離れた点の $\vec{T}$ を数学的に得るためには、 $\vec{r}$ における $\vec{T}$ の微分係数を知ればよい。今の場合、(6.2.45)式の $\vec{T}$ が二成分 $(T_{x} と T_{y})$ を持つベクトルであり変数が $x$ と $y$ であるから、 $T_{x}$ に対し二つ、 $T_{y}$ に対し二つ、すなわち

<6-98>　 $(\begin{array}{l} \frac{\partial T_{x}}{\partial x} \frac{\partial T_{x}}{\partial y} \\ \frac{\partial T_{y}}{\partial x} \frac{\partial T_{y}}{\partial y} \end{array})$

の計 $4$ 個の微分係数が必要になる。
　これらを含む量の一つに「ベクトル量の発散（ダイバージェンス）」とよばれる量がある。単位ベクトル間の内積に成り立つ関係(6.2.15)式を利用して、 $\vec{T} (\vec{r})$ の発散は、

<6-99>　(6.2.46)　 $\begin{matrix} div \vec{T} (\vec{r}) = \frac{\partial T_{x} (\vec{r})}{\partial x} + \frac{\partial T_{y} (\vec{r})}{\partial y} \\ = \frac{\partial}{\partial x} T_{x} + \frac{\partial}{\partial y} T_{y} \\ = (\vec{i} \frac{\partial}{\partial x} + \vec{j} \frac{\partial}{\partial y}) \cdot (\vec{i} T_{x} + \vec{j} T_{y}) \end{matrix}$

によって定義され、(6.2.43)式で導入されたベクトル演算子 $\nabla$ と $\vec{T}$ との内積の形で、

<6-100>　(6.2.47)　 $div \vec{T} (\vec{r}) = \nabla \cdot \vec{T}$

と形式的に書くことができる。この右辺にある書き方を使うときには注意が必要である。「 $\nabla$ はその右側にある関数の偏微分係数を作る」演算子であったから、微分される関数は必ず $\nabla$ の右側に置かなければならない。もし微分される関数を $\nabla$ の左側に置くと、説明はしないが、それは異なる意味を持つ。「ベクトルの発散」は液体、気体、電気などのように、何らかの連続した流れが存在する物理系に必ず現れ、関係する物理量がある点 $\vec{r}$ から流れ出た量とその点に流れ込んだ量の差、すなわちその点から発散した物理量を表す。それでこの量に「divergence（発散）」という名前がついているのである。

§3. 空間にある点のベクトル表現

【空間のベクトル】

　ここまでは平面にある点の位置を表す方法について考えてきたが、時には空間を運動する物理系の位置を指定しなければならない場合がある。そのような場合の位置ベクトルを表すためには、平面上で直交する単位ベクトル $\vec{i}$ と $\vec{j}$ に加えて、その面に垂直な方向の、すなわち $\vec{i}$ と $\vec{j}$ に直交する単位ベクトル $\vec{k}$ が必要になる。 $\vec{i}$ と $\vec{j}$ に垂直な方向は二つあるが、それは「右手の規則」にしたがって決める。すなわち、垂直に開いた右手の親指と人差し指に $\vec{i}$ と $\vec{j}$ を対応させ、それらに直交する中指が指す方向を $\vec{k}$ の方向とする。三つの単位ベクトル間の内積は(6.2.22)式に $\vec{k}$ を含む内積が加わる。まとめると

<6-101>　(6.3.1)　 $\{\begin{cases} \vec{i} \cdot \vec{i} = \vec{j} \cdot \vec{j} = \vec{k} \cdot \vec{k} = 1 \\ \vec{i} \cdot \vec{j} = \vec{j} \cdot \vec{k} = \vec{k} \cdot \vec{i} = 0 \end{cases}$

　 $\vec{k}$ が導入されたために、それらに関する(6.2.15)式と(6.3.1)式の内積の他に $(\vec{i}, \vec{j}, \vec{k})$ 間の外積が存在する。それを説明する前に、二つのベクトル $\vec{a}$ と $\vec{b}$ の「外積」 $\vec{a} \times \vec{b}$ の意味をもう一度思い出しておく。

【外積 $\vec{a} \times \vec{b}$ 】　外積 $\vec{a} \times \vec{b}$ はベクトルであり、その大きさは $\vec{a}$ と $\vec{b}$ を $2$ 辺とする平行四辺形の面積で与えられ、方向は「右手の規則」によって決まる。すなわち、 $\vec{a}$ と $\vec{b}$ を右手の親指と人差し指に対応させたときに、外積の方向は中指の方向で与えられる。

と定義したので、三つの単位ベクトル $(\vec{i}, \vec{j}, \vec{k})$ 間には外積、

<6-102>　(6.3.2)　 $\{\begin{cases} \vec{i} \times \vec{i} = \vec{j} \times \vec{j} = \vec{k} \times \vec{k} = 0 \\ \vec{i} \times \vec{j} = \vec{k}, \vec{j} \times \vec{k} = \vec{i}, \vec{k} \times \vec{i} = \vec{j} \end{cases}$

の関係が成り立つ。
　外積はそれを作る積の順番を入れ替えたときに符号が変わる。それを説明するには外積の方向に関する「右手の規則」と同じ内容を持つ「右ネジの規則」を使って説明するのが理解しやすい。すなわち、二つのベクトルの外積で出来るベクトルの方向は、前に置かれたベクトルから後に置かれたベクトルに向かって右ネジを回した時、ネジが進む方向である。したがって、二つのベクトルの前後を入れ替えると、右ネジを回す方向が逆転し、それが進む向きも逆転する。一方、外積を構成する二つのベクトルを入れ換えてもそれらが作る平行四辺形は変わらないから、その面積で与えられる「外積の大きさ」は変わらない。すなわち、二つのベクトル $\vec{a}$ と $\vec{b}$ の外積 $\vec{a} \times \vec{b}$ について、

<6-103>　 $\vec{b} \times \vec{a} = - \vec{a} \times \vec{b}$

が成り立つ。単位ベクトルに対しても、(6.3.2)式で積の順番を入れ換えると符号が反転する（たとえば $\vec{i} \times \vec{j} = - \vec{j} \times \vec{i}$ ）。

【余談】
小学校で九九を学んだ時、掛け算の順番に関し「 $2 \times 3 = 3 \times 2 = 6$ 」のように、二つの数を入れ換えてもその結果が変わらないことを当たり前と理解してしまうことがある。そうすると、学習が進み外積のように特殊な二つの数の積が現れた時、ほとんどの学生はそれがどのような数であっても「 $a \times b = b \times a$ 」のように、積の順序を入れ替えても結果が変わらないと無意識に思ってしまう。しかし「 $a \times b = b \times a$ 」が成り立つ数は特殊な数であって、「二つの数は順番を入れ換えて掛け算を実行した時に、一般に結果は一致しない」。すなわち「 $a \times b \neq b \times a$ 」であるのが普通である。外積は $「 a \times b \neq b \times a 」$ の一つの場合であるし、二つの行列 $A$ と $B$ に対しても一般には $A B \neq B A$ なのである。すなわち、「 $a \times b = b \times a$ 」が成り立つのは特殊な“数”である。特殊な例を最初に学ぶと、それが“普通”になり、“普通”が“特殊”になることは、必ずしも数学の世界だけではない。

　空間にあるベクトルに関しては、ほとんどの場合、これまでの平面での議論を単純に拡張するだけでよい。たとえば空間にあるベクトル $\vec{T}$ は一般に $3$ 個の成分を持ち、

<6-104>　(6.3.3)　 $\vec{T} = \vec{i} T_{1} + \vec{j} T_{2} + \vec{k} T_{3}$

と書くことができる。そのような二つのベクトル $\vec{a} = \vec{i} a_{1} + \vec{j} a_{2} + \vec{k} a_{3}$ と、 $\vec{b} = \vec{i} b_{1} + \vec{j} b_{2} + \vec{k} b_{3}$ の内積は $(\vec{a} \cdot \vec{b})$ に(6.3.1)式を機械的に適用して計算すれば、

<6-105>　(6.3.4)　 $\begin{array}{l} \vec{a} \cdot \vec{b} = (\vec{i} a_{1} + \vec{j} a_{2} + \vec{k} a_{3}) \cdot (\vec{i} b_{1} + \vec{j} b_{2} + \vec{k} b_{3}) \\ = a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3} \end{array}$

となり、二成分ベクトルの内積(6.2.14)式に第三の成分の積を加えた結果となる。これが $\vec{a}$ の大きさ $(a)$ と $\vec{b}$ の大きさ $(b)$ の積に $\vec{a}$ と $\vec{b}$ がなす角の余弦 $(cos θ)$ をかけた

<6-106>　(6.3.5)　 $\vec{a} \cdot \vec{b} = ab cos θ$

で与えられるのは二成分ベクトルの場合の(6.2.17)式と同じである。
　外積も同様に(6.3.1)式を機械的に適用して(6.3.2)式に与えられた単位ベクトルの外積の関係を正しく扱って注意深く計算すると、

<6-107>　(6.3.6)　 $\begin{array}{l} \vec{a} \times \vec{b} = (\vec{i} a_{1} + \vec{j} a_{2} + \vec{k} a_{3}) \times (\vec{i} b_{1} + \vec{j} b_{2} + \vec{k} b_{3}) \\ = \vec{i} (a_{2} b_{3} - a_{3} b_{2}) + \vec{j} (a_{3} b_{1} - a_{1} b_{3}) \\ + \vec{k} (a_{1} b_{2} - a_{2} b_{1}) \end{array}$

となる。これは各自で確かめてほしい。
　空間内の一点の位置 $\vec{r}$ を指定するためには

<6-108>　(6.3.7)　 $\vec{r} = \vec{i} x + \vec{j} y + \vec{k} z$

というように三つの座標 $(x, y, z)$ が必要になる。空間にあるベクトルを平面のベクトルと同じように平面上の図を使って示すことは不可能ではないが、結局はその図をもとにして頭の中に空間的な状況を想像することになる。

【ベクトルの発散（ダイバージェンス）】

　空間に存在する物理量がもし $\vec{r}$ の関数であれば、それは第三の座標変数 $z$ を持つので、平面で考えられた勾配や発散といった微分係数を持つ演算を少し拡張しなければならない。といっても単純に第三の変数部分を付け加えるだけである。すなわち、関数 $A (\vec{r})$ の勾配は、

<6-109>　(6.3.8)　 $\nabla A (\vec{r}) = \vec{i} \frac{\partial A}{\partial x} + \vec{j} \frac{\partial A}{\partial y} + \vec{k} \frac{\partial A}{\partial z}$

のように、平面上の勾配(6.2.42)式に $z$ に関する微分係数を成分とする $\vec{k}$ 方向のベクトルが加えられる。
　また(6.3.3)式に与えられるベクトル $\vec{T}$ の平面内の成分が $\vec{r}$ の関数であって、それに第三の成分が加わる

<6-110>　(6.3.9)　 $\vec{T} (\vec{r}) = \vec{i} T_{1} (\vec{r}) + \vec{j} T_{2} (\vec{r}) + \vec{k} T_{3} (\vec{r})$

の場合がある。このとき $\vec{T} (\vec{r})$ の発散は(6.2.46)式に第三成分の微分係数を加えて、

<6-111>　(6.3.10)　 $div \vec{T} (\vec{r}) = \frac{\partial T_{1}}{\partial x} + \frac{\partial T_{2}}{\partial y} + \frac{\partial T_{3}}{\partial z}$

となる。勾配（（6.3.8)式）と発散（(6.3.10)式）の違いにはくれぐれも注意すること：

【勾配】　勾配はスカラー関数から作られるベクトル量である。

【発散】　発散はベクトル関数から作られるスカラー量である。

(6.2.43)式に与えた平面の勾配演算子に代わり、空間に拡張された勾配演算子

<6-112>　(6.3.11)　 $\nabla = \vec{i} \frac{\partial}{\partial x} + \vec{j} \frac{\partial}{\partial y} + \vec{k} \frac{\partial}{\partial z}$

を使うと、二つのベクトルの内積が成分同士の積の和であることから $\vec{T} (\vec{r})$ の発散が

<6-113>　(6.3.12)　 $div \vec{T} (\vec{r}) = \nabla \cdot \vec{T} (\vec{r})$

とも書け、成分をあらわに書かなければ(6.2.47)式と同じ表現となる。ただし $\vec{T}$ との内積を作る時に、 $\nabla$ の成分である「微分演算子はその微分演算が右側に置かれた関数に及ぶよう、 $\vec{T}$ の左側に置かれなければならない」ことは二成分の場合と同じである。

【ベクトルの回転（ローテーション）】

　ここまでは二成分ベクトルに対して成り立つ演算の単純な拡張であったが、ベクトルが第三の成分を持つためにこれまで考えなかった量が現れる。勾配や発散の仲間で「 回転（ローテーション）」と呼ばれる量である。回転は、平面内で直線上を運動している物体が直線からそれた運動を始めたり、物体が平面から離れた運動を行うときに物理で必要になる量であるが、ここでは運動の形態を気にしなくてもよい。
　(6.3.12)式の発散がベクトル微分演算子 $\nabla$ とベクトル $\vec{T} (\vec{r})$ との内積で作られるスカラー量であったのに対して、回転（ローテーション）はベクトル微分演算子 $\nabla$ とベクトル $\vec{T} (\vec{r})$ の外積で作られるベクトル量である。ただし、 $\nabla$ が普通のベクトルではなく関数 $\vec{T} (\vec{r})$ に微分演算を行なう微分演算子であるため、 $\nabla$ を置く位置を注意深く扱う必要がある。
　普通のベクトル $\vec{a}$ と $\vec{b}$ の外積 $\vec{a} \times \vec{b}$ の場合には方向が $\vec{a}$ と $\vec{b}$ によって決まるが、回転の場合には $\nabla$ に幾何学的な方向の意味がないので、回転で出来たベクトルの方向を「右手の規則」（あるいは「右ネジの規則」）によって定めることはできない。回転ベクトルの方向は以下に与えられる三つの成分の値によってのみ定まる。 $\vec{T} (\vec{r})$ の回転は $(rot \vec{T} (\vec{r}))$ または $(\nabla \times \vec{T} (\vec{r}))$ と書かれ、それを

単位ベクトルは座標の関数ではないので座標で微分されないこと、
ベクトルの外積に関係するのは単位ベクトルだけであること、

に注意して、代数的に以下の計算を行うと

<6-114>　 $\begin{array}{l} rot \vec{T} (\vec{r}) = \nabla \times \vec{T} (\vec{r}) \\ = (\vec{i} \frac{\partial}{\partial x} + \vec{j} \frac{\partial}{\partial y} + \vec{k} \frac{\partial}{\partial z}) \\ \times (\vec{i} T_{x} + \vec{j} T_{y} + \vec{k} T_{z}) \\ = (\vec{i} \times \vec{i}) \frac{\partial T_{x}}{\partial x} + (\vec{i} \times \vec{j}) \frac{\partial T_{y}}{\partial x} + (\vec{i} \times \vec{k}) \frac{\partial T_{z}}{\partial x} \\ + (\vec{j} \times \vec{i}) \frac{\partial T_{x}}{\partial y} + (\vec{j} \times \vec{j}) \frac{\partial T_{y}}{\partial y} + (\vec{j} \times \vec{k}) \frac{\partial T_{z}}{\partial y} \\ + (\vec{k} \times \vec{i}) \frac{\partial T_{x}}{\partial z} + (\vec{k} \times \vec{j}) \frac{\partial T_{y}}{\partial z} + (\vec{k} \times \vec{k}) \frac{\partial T_{z}}{\partial z} \end{array}$

となる。ここに現れた単位ベクトルの $9$ 個の外積を(6.3.2)式を使って書き換えると、上式は

<6-115>　(6.3.13)　 $\begin{array}{l} rot \vec{T} (\vec{r}) = \vec{i} [\frac{\partial T_{z}}{\partial y} - \frac{\partial T_{y}}{\partial z}] + \vec{j} [\frac{\partial T_{x}}{\partial z} - \frac{\partial T_{z}}{\partial x}] \\ + \vec{k} [\frac{\partial T_{y}}{\partial x} - \frac{\partial T_{x}}{\partial y}] \end{array}$

となる。ただし、並びを $(x, y, z)$ 成分の順になるように外積の規則を当てはめてできた結果を適当に入れかえた。これが座標の関数に対する回転演算の結果である。

【ベクトル演算子を含むいくつかの公式】

　ここまでで、ベクトルの微分には三種の演算（勾配、発散、回転）のあることが分かった。任意のスカラー関数を $f (\vec{r})$ 、任意のベクトル関数を $\vec{a} (\vec{r})$ としてそれをまとめておく。複雑に感じるかもしれないが、もしどこかでこれらのどれかが必要になった時には、それがここにあったと思い出す程度に憶えておくだけで十分である：

【勾配】<6-116>　 $grad f (\vec{r}) = \nabla f (\vec{r}) = \vec{i} \frac{\partial f}{\partial x} + \vec{j} \frac{\partial f}{\partial y} + \vec{k} \frac{\partial f}{\partial z}$
（スカラー関数 $f$ の勾配はベクトルである。）
【発散】<6-117>　 $div \vec{a} (\vec{r}) = \nabla \cdot \vec{a} (\vec{r}) = \frac{\partial a_{x}}{\partial x} + \frac{\partial a_{y}}{\partial y} + \frac{\partial a_{z}}{\partial z}$
（発散は $\nabla$ とベクトルの内積であるから結果はスカラーになる。）
【回転】<6-118>　 $\begin{matrix} rot \vec{a} (\vec{r}) = \nabla \times \vec{a} (\vec{r}) \\ = \vec{i} (\frac{\partial a_{z}}{\partial y} - \frac{\partial a_{y}}{\partial z}) + \vec{j} (\frac{\partial a_{x}}{\partial z} - \frac{\partial a_{z}}{\partial x}) + \vec{k} (\frac{\partial a_{y}}{\partial x} - \frac{\partial a_{x}}{\partial y}) \end{matrix}$
（回転は $\nabla$ とベクトルの外積であるから結果はベクトルになる。）

　物理ではベクトル関数

\vec{T}

が座標変数

\vec{r}

に加えて他の変数を含む場合がしばしばあり、その変数で関数の様々な積を微分しなければならないときがある。以下にもう一つの変数を

t

としてそのいくつかの例をあげておくので、必要な時はここを参照するとよい。
　二つのスカラー関数（成分を持たない関数）を

f (\vec{r}, t)

と

g (\vec{r}, t)

とし、二つのベクトル関数（三つの成分を持つ関数）を

\vec{a} (\vec{r}, t)

と

\vec{b} (\vec{r}, t)

とすると：

　スカラー関数 $f (\vec{r}, t)$ とベクトル関数 $\vec{a} (\vec{r}, t)$ の積でできるベクトル関数に対して
<6-119>　(6.3.14)　 $\frac{d}{d t} (f \vec{a}) = \frac{df}{dt} \vec{a} + f \frac{d \vec{a}}{dt}$
が成り立つ。
　ベクトル関数 $\vec{a} (\vec{r}, t)$ とベクトル関数 $\vec{b} (\vec{r}, t)$ の内積 $(\vec{a} (\vec{r}, t) \cdot \vec{b} (\vec{r}, t))$ でできるスカラー関数に対して
<6-120>　(6.3.15)　 $\frac{d (\vec{a} \cdot \vec{b})}{dt} = \frac{d \vec{a}}{dt} \cdot \vec{b} + \vec{a} \cdot \frac{d \vec{b}}{d t}$
である。
　ベクトル関数 $\vec{a} (\vec{r}, t)$ とベクトル関数 $\vec{b} (\vec{r}, t)$ の外積 $[\vec{a} (\vec{r}, t) \times \vec{b} (\vec{r}, t)]$ でできるベクトル関数に対して
<6-121>　(6.3.16)　 $\begin{matrix} \frac{d}{dt} [\vec{a} \times \vec{b}] = \frac{d \vec{a}}{dt} \times \vec{b} + \vec{a} \times \frac{d \vec{b}}{dt} \end{matrix}$
である。
もし内積<6-122> $(\vec{a} (\vec{r}, t) \cdot \vec{a} (\vec{r}, t))$ が $t$ によらず一定なら、 $\vec{a} (\vec{r}, t)$ と $(\frac{\partial \vec{a} (\vec{r}, t)}{\partial t})$ は直交する[6]。すなわち、
<6-123>　(6.3.17)　 $\vec{a} (\vec{r}, t) \cdot \vec{a} (\vec{r}, t) = 一定 \Rightarrow \vec{a} \cdot (\frac{\partial \vec{a}}{\partial t}) = 0$
　 $\vec{r} = \vec{i} x + \vec{j} y + \vec{k} z$ の回転に対して、必ず
<6-124>　(6.3.18)　 $rot \vec{r} = \nabla \times \vec{r} = 0$
が成り立つ。
　もし $\vec{a} (\vec{r}, t)$ が $f (\vec{r}, t)$ を使って<6-125> $\vec{a} (\vec{r}, t) = \nabla f (\vec{r}, t)$ のように与えられていれば、 $\vec{a} (\vec{r}, t)$ の回転は必ず
<6-126>　(6.3.19)　 $rot \vec{a} = \nabla \times \vec{a} = 0$
となる。
　 $r = \sqrt{x^{2} + y^{2} + z^{2}}$ であるベクトル $\vec{r}$ と $t$ の関数 $f (\vec{r}, t)$ に対して
<6-127>　<6.3.20>　 $\begin{matrix} \nabla \cdot (\nabla f) = \frac{\partial^{2} f}{\partial x^{2}} + \frac{\partial^{2} f}{\partial y^{2}} + \frac{\partial^{2} f}{\partial z^{2}} \\ = (\frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}} + \frac{\partial^{2}}{\partial z^{2}}) f \\ \equiv Δ f \end{matrix}$
によって演算子 $Δ$ （ラプラシアン）を定義するとき、
<6-128>　(6.3.21)　 $Δ (\frac{1}{r}) = 0$
である。ラプラシアン演算子 $Δ$ をナブラ演算子 $\nabla$ と混同しないよう注意せよ。
　二つのスカラー関数 $f (\vec{r}, t)$ と $g (\vec{r}, t)$ の積で出来るスカラー関数の勾配はベクトル関数となり、それは
<6-129>　(6.3.22)　 $\nabla (f g) = f (\nabla g) + (\nabla f) g$
で与えられる。
　スカラー関数 $f (\vec{r}, t)$ とベクトル関数 $\vec{a} (\vec{r}, t)$ の積で出来るベクトル関数の発散はスカラー関数となり、それは
<6-130>　(6.3.23)　 $\nabla \cdot (f \vec{a}) = (\nabla f) \cdot \vec{a} + f (\nabla \cdot \vec{a})$
で与えられる。
　スカラー関数 $f (\vec{r}, t)$ とベクトル関数 $\vec{a} (\vec{r}, t)$ の積で出来るベクトル関数の回転はベクトル関数となり、それは
<6-131>　(6.3.24)　 $\nabla \times (f \vec{a}) = (\nabla f) \times \vec{a} + f (\nabla \times \vec{a})$
で与えられる。
　二つのベクトル関数、 $\vec{a} (\vec{r}, t)$ と $\vec{b} (\vec{r}, t)$ の外積で出来るベクトル関数の発散はスカラー関数となり、それは
<6-132>　(6.3.25)　 $\nabla \cdot [\vec{a} \times \vec{b}] = (\nabla \times \vec{a}) \cdot \vec{b} - \vec{a} \cdot (\nabla \times \vec{b})$
で与えられる。
　二つのベクトル関数、 $\vec{a} (\vec{r}, t)$ と $\vec{b} (\vec{r}, t)$ の外積で出来るベクトル関数の回転はベクトル関数となり、それは
<6-133>　(6.3.26)　 $\begin{array}{l} \nabla \times [\vec{a} \times \vec{b}] = (\vec{b} \cdot \nabla) \vec{a} - \vec{b} (\nabla \cdot \vec{a}) \\ - (\vec{a} \cdot \nabla) \vec{b} + \vec{a} (\nabla \cdot \vec{b}) \end{array}$
で与えられる。
　二つのベクトル関数、 $\vec{a} (\vec{r}, t)$ と $\vec{b} (\vec{r}, t)$ の内積でできるスカラー関数の勾配はベクトル関数となり、それは
<6-134>　(6.3.27)　 $\begin{array}{l} \nabla (\vec{a} \cdot \vec{b}) = (\vec{b} \cdot \nabla) \vec{a} + (\vec{a} \cdot \nabla) \vec{b} \\ + \vec{b} \times (\nabla \times \vec{a}) + \vec{a} \times (\nabla \times \vec{b}) \end{array}$
で与えられる。
　スカラー関数 $f (\vec{r}, t)$ の勾配で出来るベクトル関数の回転は
<6-135>　(6.3.28)　 $\nabla \times (\nabla f) = rot (grad f) = 0$
で与えられる。
　ベクトル関数 $\vec{a} (\vec{r}, t)$ の回転で出来るベクトル関数の発散は
<6-136>　(6.3.29)　 $\nabla \cdot [\nabla \times \vec{a}] = div (rot \vec{a}) = 0$
で与えられる。
　ベクトル関数 $\vec{a} (\vec{r}, t)$ の回転で出来るベクトル関数の回転は
<6-137>　(6.3.30)　 $\begin{matrix} \nabla \times [\nabla \times \vec{a}] = \nabla (\nabla \cdot \vec{a}) - \nabla^{2} \vec{a} \\ ここで \nabla^{2} \vec{a} = \frac{\partial^{2} \vec{a}}{\partial x^{2}} + \frac{\partial^{2} \vec{a}}{\partial y^{2}} + \frac{\partial^{2} \vec{a}}{\partial z^{2}} \end{matrix}$
で与えられる。

[1] ここでは複数の成分を持つ数に対する「四則演算」を詳しく与えないが、四則演算のうち、「足し算」「引き算」「掛け算」は“普通の数”とほとんど変わらず、「割り算」が“普通の数”とは最も異なる。興味があれば複素数の「割り算」を試みるとよい。それを行うと複数の成分を持つ数の性質が良くわかる。

[2] 行列ではない普通の数を $C$ としたとき、その複素共役を $C^{*}$ と書いた。これと随伴行列を混同しないように注意せよ。もっとも、普通の数を $1$ 行 $1$ 列の行列と考えれば、その随伴行列と複素共役は同じものである。

[3] 実際に電子計算機で連立一次方程式を解くときはここで述べた逆行列を使った方法は使われず、計算機が得意な繰り返し計算を基本にした「掃き出し法」と呼ばれる系統的に変数を減らす方法が使われる。

[4]　このように1列の行列で与えられるベクトルを「列ベクトル」といい、数が横1行に並ぶ「行ベクトル」と区別することもあるが、さしあたってはその区別は必要ない。ここでは(6.2.1)式のような「列ベクトル」を単にベクトルということにする。

[5] もし $(x, y)$ に対して何らかの操作（変換）を行ったとき、その結果に $x^{2}$ や $xy$ のような $x$ や $y$ の一次以外の次数が現われたら、それは一次変換ではない。

[6] この式は(6.3.15)式で $\vec{b} = \vec{a}$ とすれば簡単に証明できる。