サンプル

第五章　複数の質点から成る系の運動

　これまでは一個の物体（質点）の運動を考えてきた。しかし、第二章§2の「作用・反作用の法則で述べたように、ある物体（Ａとする）が他の物体（Ｂとする）から力を受けて運動しているとき、Ａはそれが受ける力と同じ大きさで、方向が反対の力をＢに加えている。したがって、Ａが運動している時は同時にＢも運動しているはずである。Ｂが運動するとその位置は変わり、Ｂの位置の変化はＡに及ぼす力に影響を与える。しかし、もしＡが軽い物体で、それが例えば地球のように重い物体（Ｂ）から万有引力を受けて運動しているような場合には、重いＢがＡから受ける力の影響は非常に小さくなるので、Ｂは力を受けていないと考えてもよい。そうすると「慣性の法則」から、もしＢが運動の始まる時に静止していれば、それはいつまでも静止を続け、Ｂの位置が変わることによるＡへの影響を考えなくてもよい[1]。
　ある物体が力を受けている時はそれに力を及ぼす物体が必ず（時には複数個）存在する。もし一つを除いた他の物体に対する力の影響が小さければ、あたかもその物体が単独で力を受け運動していると考えてもよい。しかし、複数の物体がすべて同じ程度の力を受け同じ様な運動をするときは、どの物体も除外して考えることは出来ない。そのような２個以上の質点（物体）から成る物理系を「多体系」という。この章では多体系の運動を考え、その場合でも「運動量保存則」と「力学的エネルギー保存則」が成立することを示す。

§1　運動方程式：全運動量と運動量保存則

　多数の質点が互いに力を及ぼし合う物理系の特徴は $2$ 個の質点から成る簡単な系にも現れる。最も簡単な場合として、 $2$ 個の質点が作用・反作用の法則にしたがう力を及ぼし合って運動する物理系を考える。 $2$ 個の質点の質量を $m_{1}$ と $m_{2}$ とし、時刻 $t$ における $m_{1}$ の位置を ${\vec{r}}_{1}$ 、 $m_{2}$ の位置を ${\vec{r}}_{2}$ とする。それらの運動は運動方程式

<5-1>　(5.1.1)　　 $\{\begin{matrix} m_{1} \frac{d^{2} {\vec{r}}_{1} (t)}{d t^{2}} = {\vec{F}}_{21} (| {\vec{r}}_{2} - {\vec{r}}_{1} |) \\ m_{2} \frac{d^{2} {\vec{r}}_{2} (t)}{d t^{2}} = {\vec{F}}_{12} (| {\vec{r}}_{1} - {\vec{r}}_{2} |) \end{matrix}$

によって記述される。ここで $m_{2}$ が $m_{1}$ におよぼす力を ${\vec{F}}_{21}$ 、 $m_{1}$ が $m_{2}$ におよぼす力を ${\vec{F}}_{12}$ と書いた。 ${\vec{F}}_{21}$ と ${\vec{F}}_{12}$ の大きさは $2$ 質点間の距離 <5-2> $(| {\vec{r}}_{1} - {\vec{r}}_{2} | = | {\vec{r}}_{2} - {\vec{r}}_{1} | \equiv r)$ によってのみ決まる。それらは作用・反作用の法則にしたがうから

<5-3>　(5.1.2)　 ${\vec{F}}_{21} (r) = - {\vec{F}}_{12} (r)$

である。作用・反作用の法則にしたがうこのような力の下で運動する $2$ つの質点から成る物理系の力学的特徴をそれらの運動方程式(5.1.1)式を使って学ぶことにする。
　最初に $2$ つの質点の運動量

<5-4>　(5.1.3)　　 $\{\begin{matrix} {\vec{p}}_{1} (t) = m_{1} \frac{d {\vec{r}}_{1} (t)}{dt} \equiv m_{1} {\vec{v}}_{1} (t) \\ {\vec{p}}_{2} (t) = m_{2} \frac{d {\vec{r}}_{2} (t)}{dt} \equiv m_{2} {\vec{v}}_{2} (t) \end{matrix}$

を使って(5.1.1)式を書き換える：

<5-5>　(5.1.4)　 $\{\begin{matrix} \frac{d {\vec{p}}_{1} (t)}{dt} = {\vec{F}}_{21} (r) \\ \frac{d {\vec{p}}_{2} (t)}{dt} = {\vec{F}}_{12} (r) \end{matrix}$

この両式を加え、(5.1.2)式を使うと

<5-6>　(5.1.5)　 $\frac{d {\vec{p}}_{1} (t)}{dt} + \frac{d {\vec{p}}_{2} (t)}{dt} = 0$

を得る。ここで二つの質点が持つ運動量の和を「全運動量」とよび、それを

<5-7>　(5.1.6)　 $\vec{P} (t) = {\vec{p}}_{1} (t) + {\vec{p}}_{2} (t)$

と書くと(5.1.5)式は

<5-8>　(5.1.7)　 $\frac{d \vec{P} (t)}{dt} = 0$

である。これは $\vec{P} (t)$ が時間によらない一定のベクトルであることを意味している。それを ${\vec{P}}_{0}$ とすれば、

<5-9>　(5.1.8)　 $\vec{P} (t) = {\vec{P}}_{0}$

である。すなわち、系の全運動量は時間によって変わらず、したがって運動をつうじて保存される：

【全運動量の保存則】作用・反作用の法則にしたがう力を受けて運動する質点系の全運動量は必ず保存する。

　「全運動量の保存則」はもう一つの意味を持っている。二つの質点系の質量中心の座標

<5-10>　(5.1.9)　 $\vec{R} (t) = \frac{m_{1} {\vec{r}}_{1} (t) + m_{2} {\vec{r}}_{2} (t)}{m_{1} + m_{2}}$

の時間微分を計算すると、

<5-11>　 $\begin{matrix} \frac{d \vec{R}}{dt} = \frac{m_{1}}{m_{1} + m_{2}} \frac{d {\vec{r}}_{1}}{dt} + \frac{m_{2}}{m_{1} + m_{2}} \frac{d {\vec{r}}_{2}}{dt} \\ = \frac{1}{m_{1} + m_{2}} ({\vec{p}}_{1} + {\vec{p}}_{2}) \\ = \frac{1}{m_{1} + m_{2}} \vec{P} \end{matrix}$

であるから、 $\vec{P}$ を

<5-12>　(5.1.10)　 $\vec{P} (t) = (m_{1} + m_{2}) \frac{d \vec{R} (t)}{dt}$

と表すことができる。そうすると(5.1.8)式の $\vec{P}$ が一定であるということは $\frac{d \vec{R} (t)}{dt}$ が一定であることを意味し、系の質量中心である $\vec{R}$ が等速度で運動することと同じ意味を持っていることがわかる。すなわち

作用・反作用の法則にしたがう力の下で運動する質点系の全運動量は保存し、それは系の質量中心が一定速度で運動することを意味する。

　多数の質点からなる系でも、もし質点に働く全ての力が作用・反作用の法則にしたがえば、その質量中心はやはり一定速度で運動することを証明することができる。少し複雑であるがその大体の様子を示すことにする。

N

個の質点から成る系を考え、それらの質量を

(m_{1}, m_{2}, \dots, m_{N})

とする。

m_{1}

には

1

以外の全ての質点から力が働き、

m_{2}

には

2

以外の全ての質点から力が働き、……なので、

m_{1}

と

m_{2}

の距離を

r_{21}

、

m_{1}

と

m_{3}

の距離を

r_{31}

、…とすれば、

(m_{1}, m_{2}, \dots, m_{N})

に対する運動方程式は

<5-13>　(5.1.11)　 $\{\begin{matrix} m_{1} \frac{d^{2} {\vec{r}}_{1} (t)}{d t^{2}} = {\vec{F}}_{21} (r_{21}) + {\vec{F}}_{31} (r_{31}) + \dots + {\vec{F}}_{N 1} (r_{N 1}) \\ m_{2} \frac{d^{2} {\vec{r}}_{2} (t)}{d t^{2}} = {\vec{F}}_{12} (r_{12}) + {\vec{F}}_{32} (r_{32}) + \dots + {\vec{F}}_{N 2} (r_{N 2}) \\ \dots \dots \dots \dots \dots \\ m_{N} \frac{d^{2} {\vec{r}}_{N} (t)}{d t^{2}} \\ = {\vec{F}}_{1 N} (r_{1 N}) + {\vec{F}}_{2 N} (r_{2 N}) + \dots + {\vec{F}}_{N - 1, N} (r_{N - 1, N}) \end{matrix}$

である。ここで、 ${\vec{F}}_{ij}$ の添え字は $j$ 番目の質点が $i$ 番目の質点から受ける力を表す。これらの式を運動量

<5-14>　(5.1.12)　　 $\{\begin{matrix} {\vec{p}}_{1} (t) = m_{1} \frac{d {\vec{r}}_{1} (t)}{dt} \equiv m_{1} {\vec{v}}_{1} (t) \\ {\vec{p}}_{2} (t) = m_{2} \frac{d {\vec{r}}_{2} (t)}{dt} \equiv m_{2} {\vec{v}}_{2} (t) \\ \dots\dots\dots\dots\dots \\ {\vec{p}}_{N} (t) = m_{N} \frac{d {\vec{r}}_{N} (t)}{dt} \equiv m_{N} {\vec{v}}_{N} (t) \end{matrix}$

を使って表すと

<5-15>　(5.1.13)　　 $\{\begin{matrix} \frac{d {\vec{p}}_{1} (t)}{dt} = {\vec{F}}_{21} (r_{21}) + {\vec{F}}_{31} (r_{31}) + \dots + {\vec{F}}_{N 1} (r_{N 1}) \\ \frac{d {\vec{p}}_{2} (t)}{dt} = {\vec{F}}_{12} (r_{12}) + {\vec{F}}_{32} (r_{32}) + \dots + {\vec{F}}_{N 2} (r_{N 2}) \\ \dots\dots\dots\dots\dots \\ \frac{d {\vec{p}}_{N} (t)}{dt} = {\vec{F}}_{1 N} (r_{1 N}) + {\vec{F}}_{2 N} (r_{2 N}) + \dots + {\vec{F}}_{N - 1, N} (r_{N - 1, N}) \end{matrix}$

となる。この左辺の和を右辺の和に等値すると、作用・反作用の法則

<5-16>　(5.1.14)　 ${\vec{F}}_{ij} (r_{ij}) = - {\vec{F}}_{ji} (r_{ji}) = - {\vec{F}}_{ji} (r_{ij})$

から(5.1.13)式右辺の和は全て相殺して $0$ となるので、

<5-17>　(5.1.15)　 $\frac{d \vec{P} (t)}{dt} = 0$

を得る。ここで

<5-18>　(5.1.16)　 $\vec{P} (t) = {\vec{p}}_{1} (t) + {\vec{p}}_{2} (t) + \dots + {\vec{p}}_{N} (t)$

は $N$ 個の質点が持つ運動量の和（全運動量）である。したがって $2$ 質点系と同じようにこの系の全運動量は保存する。運動量を(5.1.12)式を使って座標に書き換え、全運動量を $N$ 質点の質量中心の座標

<5-19>　(5.1.17)　 $\vec{R} (t) = \frac{m_{1} {\vec{r}}_{1} (t) + m_{2} {\vec{r}}_{2} (t) + \dots + m_{N} {\vec{r}}_{N} (t)}{m_{1} + m_{2} + \dots + m_{N}}$

を使って表せば、

<5-20>　(5.1.18)　 $\vec{P} (t) = (m_{1} + m_{2} + \dots m_{N}) \frac{d \vec{R} (t)}{dt}$

である。したがって、やはり $\vec{P}$ の保存は $N$ 個の質点系の質量中心が等速度で運動することを表している。すなわち

$N$ 個の質点系が作用・反作用の法則にしたがう力の下で運動するとき、質点系の全運動量は保存し、それは系の質量中心が一定速度で運動することを意味する。

自然界に存在する全ての力は例外なく作用・反作用の法則に従うと考えられている[2]。したがって自然界で運動する物理系を観測すればその全運動量は保存し、質量中心は等速運動をするはずである。実際にこれまでこの結論と矛盾する観測結果は報告されておらず、確かに観測の結果は自然界で私たちが知っている全ての力は作用・反作用の法則に従うことを示している。もし観測した結果が「全運動量の保存則」を乱していれば、そこには全運動量を保存させるような残りの運動量を持った、私たちが未だ知らない物体が存在しなければならない。

§2　質量中心の運動と相対的な運動

　前節で「作用・反作用の法則にしたがう力の下で運動する質点系の全運動量は保存し、系の質量中心は一定速度で運動する」ことを知った。この事実を利用すると、多くの質点を含む物理系の運動から質量中心の運動を分けて扱うことができ、問題の扱いを簡単にすることができる。それを示すために再び作用・反作用の法則にしたがい力をおよぼし合う質量 $m_{1}$ と $m_{2}$ を持つ $2$ 質点の運動を考える。それらの運動方程式は(5.1.1)式であり、それらが受ける力は(5.1.2)式を満足する。このとき系の全運動量は保存し、したがって(5.1.9)式で与えられる質量中心は一定の速度で運動することを知った。ここではこの $2$ 質点系の運動をあらためて少し詳しく調べる。
　質点に働く力（(5.1.1)式の右辺）は $2$ 質点間の距離の関数であるから、それを

<5-21>　(5.2.1)　 ${\vec{r}}_{1} (t) - {\vec{r}}_{2} (t) \equiv \vec{r} (t)$

とする。したがって、 $| \vec{r} | \equiv r$ と置くと運動方程式は

<5-22>　(5.2.2)　　 $\{\begin{matrix} m_{1} \frac{d^{2} {\vec{r}}_{1} (t)}{d t^{2}} = {\vec{F}}_{21} (r) \\ m_{2} \frac{d^{2} {\vec{r}}_{2} (t)}{d t^{2}} = {\vec{F}}_{12} (r) \end{matrix}$

と書くことができた。二つの式を加えることによって「運動量の保存則」が得られたが、ここでは第一の式に $m_{2}$ をかけた式から第二の式に $m_{1}$ をかけた式を引き算する。そうすると、 ${\vec{F}}_{12} = - {\vec{F}}_{21}$ であるから、あらためて <5-23> $({\vec{F}}_{21} (r) \equiv \vec{F} (r))$ と書けば

<5-24>　 $m_{1} m_{2} \frac{d^{2} \vec{r} (t)}{d t^{2}} = (m_{1} + m_{2}) \vec{F} (r)$

を得る。したがって、

<5-25>　(5.2.3)　 $μ = \frac{m_{1} m_{2}}{m_{1} + m_{2}}$

と置けば、この式は

<5-26>　(5.2.4)　 $μ \frac{d^{2} \vec{r} (t)}{d t^{2}} = \vec{F} (r)$

となる。これは、質量 $μ$ を持つ仮想的な質点があり、それが $r = 0$ にある力の源から力 $\vec{F}$ を受けて行う運動を表す方程式の形をしている。この $μ$ を質量が $m_{1}$ と $m_{2}$ の系の「換算質量」という。
　一方、(5.1.10)式で与えられるこの系の全運動量に対して(5.1.7)式が成り立つから、質量中心には

<5-27>　(5.2.5)　 $M \frac{d^{2} \vec{R}}{d t^{2}} = 0$

が成り立つ。

　以上をまとめると、

$2$ 質点が作用・反作用の法則にしたがう力 $\vec{F}$ の下で運動するとき、 $2$ 質点の運動方程式

<5-28>　 $\{\begin{matrix} m_{1} \frac{d^{2} {\vec{r}}_{1} (t)}{d t^{2}} = {\vec{F}}_{21} (| {\vec{r}}_{1} - {\vec{r}}_{2} |) \\ m_{2} \frac{d^{2} {\vec{r}}_{2} (t)}{d t^{2}} = {\vec{F}}_{12} (| {\vec{r}}_{2} - {\vec{r}}_{1} |) \end{matrix}$

はそれらと同等の二つの方程式

<5-29>　 $\{\begin{matrix} M \frac{d^{2} \vec{R} (t)}{d t^{2}} = 0 \\ μ \frac{d^{2} \vec{r} (t)}{d t^{2}} = \vec{F} (r) \end{matrix}$

に書き換えられる。ここで、 $M = m_{1} + m_{2}$ は全質量、および、 $μ = \frac{m_{1} m_{2}}{m_{1} + m_{2}}$ は換算質量であり、「質量中心の座標」 $\vec{R} (t)$ と「相対座標」 $\vec{r} (t)$ は

<5-30>　(5.2.6)　 $\{\begin{matrix} \vec{R} (t) = \frac{m_{1} {\vec{r}}_{1} (t) + m_{2} {\vec{r}}_{2} (t)}{m_{1} + m_{2}} \\ \vec{r} (t) = {\vec{r}}_{1} (t) - {\vec{r}}_{2} (t) \end{matrix}$

によって定義される。また $\vec{F} (r)$ は<5-31> $(\vec{F} (r) \equiv {\vec{F}}_{21} (| {\vec{r}}_{1} - {\vec{r}}_{2} |) = - {\vec{F}}_{12} (| {\vec{r}}_{2} - {\vec{r}}_{1} |))$ である。

すなわち、(5.2.5)式が意味するように、この物理系の質量中心は力の詳細によらず等速度運動を行い、力の全ての特徴は換算質量

μ

を持つ一個の質点の運動にだけ反映されるので、我々はその運動を知るだけでよい。さらに、もし力の方向が二つの質点を結ぶ方向（すなわち

\vec{r}

の方向）に沿っていれば、その力は

r = 0

に力の源を持つ中心力と同じ性質を持つので、この質点の運動は一つの平面内で行われ、それを知ることはさらに簡単になる。
　「質量中心は必ず等速度運動を行う」という

2

質点系に対する結論が、作用・反作用の法則にしたがう力の下で運動する多くの質点を含む系に対しても成立することはすでに(5.1.15)式と(5.1.18)式で示した。
　最後に、後の章の議論に使うので、二つの質点系の全運動エネルギーが二つの仮想的な粒子の運動エネルギーの和として書けることを示しておく。仮想的粒子の一つは全質量

(M = m_{1} + m_{2})

を持ち、一定の速度

\frac{d \vec{R}}{dt}

で等速度運動をし、もう一つの仮想的粒子は換算質量

(μ = \frac{m_{1} m_{2}}{m_{1} + m_{2}})

を持ち、一般に時間によって変わる速度

\frac{d \vec{r}}{dt}

で運動する。それを明確に表すために (5.2.6)式を使って

{\vec{r}}_{1}

と

{\vec{r}}_{2}

を

\vec{R}

と

\vec{r}

で表す。その結果は

<5-32>　(5.2.7)　 $\{\begin{matrix} {\vec{r}}_{1} = \vec{R} + \frac{m_{2}}{M} \vec{r} \\ {\vec{r}}_{2} = \vec{R} - \frac{m_{1}}{M} \vec{r} \end{matrix}$

である。
　時間微分に関してもこれと同様な関係が成り立つので、 $2$ 質点の運動エネルギーを

<5-33>　(5.2.8)　 $\begin{matrix} \frac{m_{1} {\vec{v}}_{1}^{2}}{2} + \frac{m_{2} {\vec{v}}_{2}^{2}}{2} = \frac{m_{1}}{2} {(\frac{d \vec{R}}{dt} + \frac{m_{2}}{M} \frac{d \vec{r}}{dt})}^{2} + \frac{m_{2}}{2} {(\frac{d \vec{R}}{dt} - \frac{m_{1}}{M} \frac{d \vec{r}}{dt})}^{2} \\ = \frac{M}{2} {(\frac{d \vec{R}}{dt})}^{2} + \frac{μ}{2} {(\frac{d \vec{r}}{dt})}^{2} \end{matrix}$

と表すことができる。最後の式の第一項目は、速度 $\frac{d \vec{R}}{dt}$ を持つ質量 $M$ の粒子の運動エネルギーであり、第二項目は、速度 $\frac{d \vec{r}}{dt}$ を持つ質量 $μ$ の粒子の運動エネルギーである。
　このように、二質点系の全運動エネルギーは、全質量 $(M = m_{1} + m_{2})$ を持ち等速 $\frac{d \vec{R}}{dt}$ で運動する質点の運動エネルギーと、換算質量 $(μ = \frac{m_{1} m_{2}}{m_{1} + m_{2}})$ を持ち時間によって変わる速度 $\frac{d \vec{r}}{dt}$ で運動する質点の運動エネルギーの和として書き換えられる。これから重要な結論が導かれる。

【結論】

質点間に働く力が作用・反作用の法則にしたがえば、二つの質点の運動を力によって影響されない質量中心の運動と、力を受けて運動する質点の運動に分離することができる。

この結論はこの後の「連成振動」や「衝突」を学ぶときに使われる。

§3　連成振動と基準振動

　前節で学んだことが実際に重要な役割をはたす自然現象に「連成振動」と呼ばれる振動形態がある（図5.1）。連成振動は運動が質量中心の運動と相対座標の運動に分離できる系であると同時に、自然が持つ基本的かつ重要な振動の形態を示す簡単な例でもあるので、最も簡単な模型的物理系を使ってそれを示すことにする。
　使う物理系は、両端に壁を持つ滑らかで水平な床と、 $2$ 個の質点と、同じ材質で出来た同じ長さの $3$ 本のバネから成る。まずバネの一本を使い $2$ 個の質点をつなぎ、それを滑らかな床の上に置く。そして、それぞれの質点をそれに近い側の壁に残りの二本のバネでつなぐ。その状態で、 $2$ 個の質点は両端に壁を持つ滑らかな床の上に等間隔に並んでいる。その系と質点の運動の様子を図5.1に描き、その下に図の詳しい説明を与えた。

（図5.1）【連成振動】

以下に図5.1に描かれた図の説明を与える。

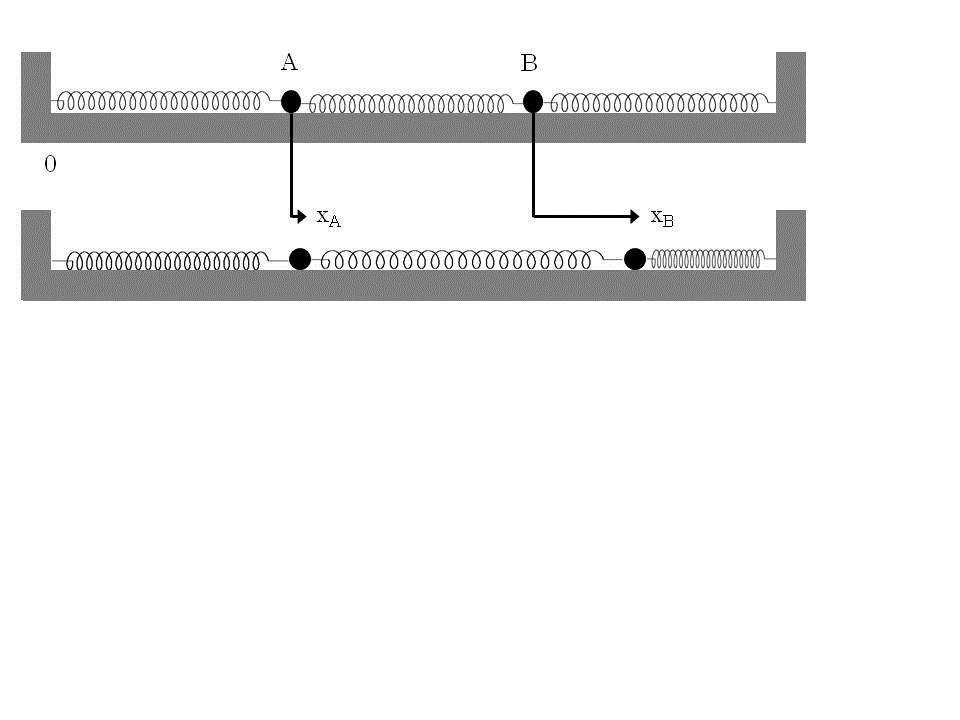
【（図5.1）の説明】
　水平で横長の長方形の両端に縦長の長方形が乗った外形を持つ図が二つ、上下に描かれている。横長の長方形は滑らかな床を表し、縦長の長方形は壁を表す。
　上の図には、横長の長方形の上に同じ大きさを持つ小球が二つ、左右にある縦長の長方形と小球の間が同じ間隔になるようにして置かれており、左右の壁と小球を $3$ 本の同じ長さのらせんがつないでいる。らせんは伸び縮みしていないバネを表している。左側の小球の上にはそれを表す文字 $A$ が記され、右側の小球の上にはそれを表す文字 $B$ が記されている。
　　下の図も上の図と同じ外形に二つの小球と、それらを両側の壁とつなぐ $3$ 本のバネが描かれているが、二つの小球が僅かに右側に移動して描かれている。図では右側の小球 $B$ の移動距離が左側の小球 $A$ の移動距離よりも大きく描かれている。その結果、上の図に描かれたバネと比べ、左側の壁と $A$ をつなぐバネは伸び、 $A$ と $B$ をつなぐバネも伸び、右側の壁と $B$ をつなぐバネは縮んで描かれている。

下の図に描かれた $3$ 本のバネは自然長から伸び縮みしているので、第三章§１で学んだフックの法則にしたがって、 $2$ つの小球にはそれぞれのバネから(3.1.3)式で与えられる力が働く。今の場合は $3$ 個のバネがあるので、小球に働く力も少し複雑になる。それをていねいに与えよう。
　二つの小球（ $A$ と $B$ ）は同じ質量を持ち、その一個の質量を $m$ 、バネの弾性定数を $k$ 、バネの自然長を $ℓ$ とする。図にあるように、二本のバネの一端は両側の壁に固定され、他端に $A$ と $B$ がつけられている。さらに $A$ と $B$ は二本のバネと同じ弾性定数と長さを持つもう一本のバネでつながれている。両側の壁の距離は $3 ℓ$ である。二つの小球あるいは一方の小球をバネの自然長の位置からどちら側にでもずらして手を放すと $A$ と $B$ は壁の間で振動を始める。そのような振動をしている状態で時刻 $t$ における $A$ と $B$ の位置が図5.1下の図のようにそれぞれの静止位置から移動した距離にあるとする。図では $A$ も $B$ も右側に移動しているが、もし物体の移動が静止位置から右側なら静止位置からの変位は正、もし物体の移動が静止位置から左側なら静止位置から変位は負と約束しておく。そして $A$ の変位を $x_{A}$ 、 $B$ の変位を $x_{B}$ と書く。そうすると、左端から第一のバネの伸びは $x_{A}$ 、第二のバネの伸びは $x_{B} - x_{A}$ 、第三のバネの伸びは $x_{B}$ である。もしバネの伸びが正ならバネは伸びた状態にあるが、それが負ならバネは縮んでいる状態を表すことに注意せよ。この状態で $A$ と $B$ にはフックの法則に従った力がバネから働く。それらは

【 $A$ に働く力】
　 $A$ には第一のばねと第二のばねから力が働く。第一のバネから働く力を $F_{A}$ 、第二のバネから働く力を $f_{A}$ とする。
　第一のバネは $A$ の変位と同じだけ自然長 $ℓ$ から伸び縮みするから、 $A$ には第一のバネからその変位の大きさに比例した大きさを持つ力 $k | x_{A} |$ が働く。もし $x_{A} > 0$ であれば（バネが伸びていれば）バネは $A$ を左側に引くから、 $(F_{A} = - k | x_{A} |)$ であり、もし $x_{A} < 0$ であれば（バネが縮んでいれば）バネは $A$ を右側に押すから、 $(F_{A} = + k | x_{A} |)$ である。したがって、結局 $F_{A} = - k x_{A}$ と書くことができる。
　第二のバネは長さが $x_{B} - x_{A}$ だけ自然長 $ℓ$ から変化しているから、 $A$ にはその大きさに比例した大きさの力 $k | x_{B} - x_{A} |$ の力が働く。その力は、もし $x_{B} > x_{A}$ ならば（バネが伸びていれば）バネは $A$ を右側に引くから、 $(f_{A} = + k | x_{B} - x_{A} |)$ であり、もし $x_{B} < x_{A}$ ならば（バネが縮んでいれば）バネは $A$ を左側に押すから、 $(f_{A} = - k | x_{B} - x_{A} |)$ である。したがって、結局その力を $f_{A} = k (x_{B} - x_{A})$ と書くことができる。

【 $B$ に働く力】
　 $B$ には第二のバネと第三のバネから力が働く。第二のバネから働く力を $f_{B}$ 、第三のバネから働く力を $F_{B}$ とする。
　第二のバネの長さ変化は上の場合と同じであるが、 $B$ に対する力の働き方は $A$ と逆向きになる。すなわち、もし $x_{B} > x_{A}$ ならば（バネが伸びていれば）バネは $B$ を左側に引くから、力は $f_{B} = - k | x_{B} - x_{A} |$ であり、もし $x_{B} < x_{A}$ ならば（バネが縮んでいれば）バネは $B$ を右側に押すので、 $f_{B} = + k | x_{B} - x_{A} |$ である。したがって $f_{B} = - k (x_{B} - x_{A})$ と書くことができる。
　第三のバネからはその伸びに比例した大きさ $k | x_{B} |$ の力が $B$ に働く。その力は、もし $x_{B} > 0$ ならば（バネが縮んでいれば）バネは $B$ を左側に押すので $(F_{B} = - k | x_{B} |)$ であり、もし $x_{B} < 0$ であれば（バネが伸びていれば）バネは $B$ を右側に引くので、 $(F_{B} = + k | x_{B} |)$ であり、結局その力を $F_{B} = - k x_{B}$ と書くことができる。

　以上から、 $A$ と $B$ に対する運動方程式は

<5-34>　(5.3.1)　 $\begin{matrix} m \frac{d^{2} x_{A}}{d t^{2}} = F_{A} + f_{A} \\ = - k x_{A} + k (x_{B} - x_{A}) \\ = - 2 k x_{A} + k x_{B} \end{matrix}$

<5-35>　(5.3.2)　 $\begin{matrix} m \frac{d^{2} x_{B}}{d t^{2}} = F_{B} + f_{B} \\ = - k x_{B} - k (x_{B} - x_{A}) \\ = k x_{A} - 2 k x_{B} \end{matrix}$

となる。この二つの式を前節で与えた二つの物体に対する質量中心の位置と相対距離を使って表すことができる。 $A$ と $B$ の位置座標は $(ℓ + x_{A})$ と $(2 ℓ + x_{B})$ であるから、それらの質量中心の座標は<5-36> $(\frac{(ℓ + x_{A}) + (2 ℓ + x_{B})}{2} = \frac{x_{A} + x_{B}}{2} + \frac{3}{2} ℓ)$ であり、相対距離は<5-37> $((2 ℓ + x_{B}) - (ℓ + x_{A}) = x_{B} - x_{A} + ℓ)$ である。 $A$ と $B$ の質量が等しいことから質量中心の座標に $A$ と $B$ の質量が現れていないことに注意せよ。
　 $A$ と $B$ が振動を始める前は、それらの質量中心はバネの全長 $3 ℓ$ の中間点 $\frac{3 ℓ}{2}$ にあり、相対距離は第二のバネの自然長 $ℓ$ である。 $2$ 球の運動を理解しやすくするために、もう一工夫する。すなわち、質量中心の静止位置と相対距離の代わりに、バネの伸び縮みによって質量中心がその静止位置からどれだけ動いたかを表す量 $X$ と、バネの伸び縮みによって $2$ 球の相対距離がどれだけ変化したかを表す量 $x$ を使うことにする。それらは

<5-38>　(5.3.3)　 $\{\begin{matrix} X = \frac{(x_{A} + ℓ) + (x_{B} + 2 ℓ)}{2} - \frac{3 ℓ}{2} \\ = \frac{x_{A} + x_{B}}{2} \\ x = (x_{B} - x_{A} + ℓ) - ℓ \\ = x_{B} - x_{A} \end{matrix}$

で定義されるから、(5.3.1)式と(5.3.2)式を一つは加え、一つは引くことによって、

X (t)

と

x (t)

が満足する方程式

<5-39>　(5.3.4)　 $M \frac{d^{2} X}{d t^{2}} = - 2 kX$

<5-40>　(5.3.5)　 $μ \frac{d^{2} x}{d t^{2}} = - \frac{3 k}{2} x$

を得る。ここで $M = 2 m$ は $A$ と $B$ の質量の和、 $μ = \frac{m}{2}$ は $A$ と $B$ の換算質量である。
　この二つの式に含まれる定数に対して適当な読みかえをすると、第三章で学んだ単振動の運動方程式である(3.1.4)式と(3.1.6)式が現れる。すなわち、(5.3.4)式の $M$ を $m$ 、 $(2 k)$ を $k$ と読みかえれば、(5.3.4)式は(3.1.4)式と一致し、(5.3.5)式の $μ$ を $m$ 、 $(\frac{3 k}{2})$ を $k$ と読みかえれば、(5.3.5)式は(3.1.6)式と一致する。したがって、(5.3.4)式の解は(3.1.4)式の解である(3.1.6)式によって与えられる。すなわち、質量中心の位置を与える(5.3.4)式の解は

<5-41>　(5.3.6)　 $X (t) = A sin (Ω t + B)$

である。ただし、今の場合は<5-42> $(Ω = \sqrt{\frac{2 k}{M}})$ と読み変えないといけない。さらに、 $2$ 球の相対距離の変化を与える(5.3.5)式の解は第三章の(3.1.6)式で与えられ、それは

<5-43>　(5.3.7)　 $x (t) = a sin (ω t + b)$

である。ただし<5-44> $(ω = \sqrt{\frac{3 k}{2 μ}})$ である。以上で $(A, B, a, b)$ は実際の運動状況から決まる定数である。 $A$ と $B$ の位置座標 $x_{A}$ と $x_{B}$ は、(5.3.3)式から与えられる関係式

<5-45>　(5.3.8)　 $\{\begin{matrix} x_{A} = X - \frac{x}{2} \\ x_{B} = X + \frac{x}{2} \end{matrix}$

に(5.3.6)式と(5.3.7)式を代入すると得られ、それらは

<5-46>　(5.3.9)　 $\{\begin{matrix} x_{A} = A sin (Ω t + B) - \frac{a}{2} sin (ω t + b) \\ x_{B} = A sin (Ω t + B) + \frac{a}{2} sin (ωt + b) \end{matrix}$

となる。
　 $(A, B, a, b)$ に具体的な数値を適当に与えて(5.3.9)式を実際に計算すればわかるが、(5.3.9)式で表される $A$ と $B$ の運動は一般に非常に複雑で、そこから(5.3.6)式や(5.3.7)式のような、単純な単振動の様子を読み取ることはとてもできない。この複雑な振動は $A$ と $B$ をつなぐバネの存在によって生じていることは、(5.3.1)式および(5.3.2)式の右辺にある $A$ と $B$ をつなぐバネからの力（第二項目）を取り除くと、(5.3.1)式右辺と(5.3.2)式右辺にある $f_{A}$ と $f_{B}$ がなくなり、その結果、両式は $A$ と $B$ の独立な単振動を表すことから理解出来るであろう。
　しかしながら、 $A$ と $B$ をつなぐバネが存在する場合であっても、複雑な振る舞いを示す(5.3.9)式を(5.3.6)式と(5.3.7)式によって表せば、 $A$ と $B$ の複雑な運動が実は二つの単純な単振動の組み合わせであることがわかる。このように、複雑な振動をおこなう系を異なる変数を使って表現すると、それを独立した単振動に分解できることがある。そのように分解された単振動をこの物理系の「基準振動」、そのときに(5.3.6)式と(5.3.7)式のように分解された単振動に現れれる角速度 $Ω$ と $ω$ を「基準振動数」と言い[3]、単振動を行う変数（今の場合は $X$ と $x$ ）をこの振動系の「基準座標」と言う。

§4　衝突

　複数の質点あるいは物体から成る系で生じる最も重要な物理現象が「衝突}」である。二つの物体が接近し、力を及ぼし合った結果それまでの運動状態（位置と速度）を変える現象を物理では「衝突」という。
　「慣性の法則」によって、どのような物体も力を受けなければ運動状態を変えることはない。したがって、もし物体の速度が変わったとすると、それは物体に力が働いた証拠である。さらに、二つの物体が速度を変えたとき、もし全運動量が変わらなければ、物体に働いた力は「作用・反作用の法則」にしたがう力であったことがわかる。
　ところが「衝突」という言葉を聞いて思い浮かべるのは、人が歩道で他の人とぶつかることであったり、自動車どうしの衝突を考え、衝突が二つの物体の間に力が働いて運動状態が変わる現象であるとはなかなか思えない。しかし二つの物体が運動状態を変えたのであるから、それらの間には必ず力が働いたはずである。なぜ日常の衝突で力が働いたように感じられないのか。それには理由がある。
　私たちが日常的に知る力は質量をもつ物体の間に働く重力（万有引力）や、電気を帯びた物体の間に働く電気力や、磁石の間に働く磁力である。ところが、これらの力は二つの物体がどんなに遠くに離れていても働く特別な力なのである。自然界には、これらの力の他に二つの物体がとても近くに接近しなければ働かない力がある。この力は働いたときにはとても強く働く。そのために、その力が働いた時はあたかも物体が接触して、瞬間的に運動状態を変えたように感じる。ここで考えている衝突に関係する力はこのような性質を持つ力の一つ（「分子間力」と呼ばれる力）なのである。いうまでもなく、この力も「作用・反作用の法則」にしたがう。したがって、この力が働いて運動する物理系の全運動量は保存する。
　衝突によって物体が持つ全運動量は変わらないが、衝突の前後で二つの物体が持つ運動エネルギーの総量が変化する衝突と変化しない衝突がある。

衝突の前後で運動エネルギーが変化しない衝突を「弾性衝突」という。
衝突の前後で運動エネルギーが変化する衝突を「非弾性衝突」という。

非弾性衝突が起きると、二つの物体が持つ運動エネルギーの総量は一般に減少するが、その減少した分は衝突した物体を構成する分子に分配され、その結果物体が変形したり壊れたりする。
　衝突の際、二つの物体の間に働く力は二つの物体が接したときにしか働かず、物体が少しでも離れれば力は働いていないと考えて良い[4]。したがって衝突の前後に二つの物体が離れていれば２つの物体は「慣性の法則」によって等速度運動をする。
　§2で学んだ「運動量保存の法則」にしたがえば、物体が互いに力を及ぼし合っていようがいまいが、質量中心の運動は衝突によって影響されず、質量中心は変わらぬ速度で運動を続け、相対距離に関する運動（相対運動）だけが衝突の影響を受ける。さらに§2では二つの物体の運動エネルギーが質量中心の運動エネルギーと相対運動の運動エネルギーの和として表されることを学んだ（(5.2.8)式）。したがって、もし衝突により

2

つの物体のエネルギーが変化するとすれば、その変化は相対運動のエネルギー変化として表われることになる。
　いま衝突する

2

物体（あるいは質点）の質量を

m_{1}

と

m_{2}

とする。そうすると、それらの質点の相対距離

\vec{r}

と質量中心の位置

\vec{r}

は

<5-47>　(5.4.1)　 $\{\begin{matrix} \vec{r} = {\vec{r}}_{1} - {\vec{r}}_{2} \\ \vec{R} = \frac{m_{1} {\vec{r}}_{1} + m_{2} {\vec{r}}_{2}}{m_{1} + m_{2}} \end{matrix}$

である。衝突前の $2$ 物体の速度を $\frac{d {\vec{r}}_{1}}{dt} = {\vec{v}}_{1}$ と $\frac{d {\vec{r}}_{2}}{dt} = {\vec{v}}_{2}$ とすると、それらの相対運動の速度 $\vec{v}$ と質量中心の速度 $\vec{V}$ は

<5-48>　(5.4.2)　 $\{\begin{matrix} \vec{v} = {\vec{v}}_{1} - {\vec{v}}_{2} \\ \vec{V} = \frac{m_{1} {\vec{v}}_{1} + m_{2} {\vec{v}}_{2}}{M} \end{matrix}$

である。ここで $M = m_{1} + m_{2}$ である。この式から、 $\vec{V}$ と $\vec{v}$ を使って ${\vec{v}}_{1}$ と ${\vec{v}}_{2}$ を表すことができる。その結果は

<5-49>　(5.4.3)　 $\{\begin{matrix} {\vec{v}}_{1} = \vec{V} + \frac{m_{2}}{M} \vec{v} \\ {\vec{v}}_{2} = \vec{V} - \frac{m_{1}}{M} \vec{v} \end{matrix}$

となる。したがって、衝突前に $2$ つの質点が持つ運動エネルギーの和を $K$ とすると、 $K$ は

<5-50>　(5.4.4)　 $\begin{matrix} K = \frac{m_{1}}{2} {\vec{v}}_{1}^{2} + \frac{m_{2}}{2} {\vec{v}}_{2}^{2} \\ = \frac{m_{1}}{2} {(\vec{V} + \frac{m_{2} \vec{v}}{M})}^{2} + \frac{m_{2}}{2} {(\vec{V} - \frac{m_{1} \vec{v}}{M})}^{2} \\ = \frac{M}{2} {\vec{V}}^{2} + \frac{m_{1} m_{2}}{2 (m_{1} + m_{2})} {\vec{v}}^{2} \\ = \frac{M}{2} {\vec{V}}^{2} + \frac{μ}{2} {\vec{v}}^{2} \end{matrix}$

と表される（(5.2.8)式と同じ式）。ここで $μ$ は換算質量（(5.2.6)式）である。
　衝突によって $2$ 質点の全運動量は変わらないが、それぞれの運動量は変化し、したがってそれぞれの速度も変わる。衝突後の $2$ 質点の速度を ${\vec{v}}_{1}^{'}$ と ${\vec{v}}_{2}^{'}$ とする。そうすると衝突後の2質点の相対運動の速度 ${\vec{v}}^{'}$ および質量中心の速度 ${\vec{V}}^{'}$ は(5.4.2)式と同じように

<5-51>　(5.4.5)　 $\{\begin{matrix} {\vec{v}}^{'} = {\vec{v}}_{1}^{'} - {\vec{v}}_{2}^{'} \\ {\vec{V}}^{'} = \frac{m_{1} {\vec{v}}_{1}^{'} + m_{2} {\vec{v}}_{2}^{'}}{M} \end{matrix}$

である。これから、衝突後の $2$ 質点の速度を求めると

<5-52>　(5.4.6)　 $\{\begin{matrix} {\vec{v}}_{1}^{'} = {\vec{V}}^{'} + \frac{m_{2}}{M} {\vec{v}}^{'} \\ {\vec{v}}_{2}^{'} = {\vec{V}}^{'} - \frac{m_{1}}{M} {\vec{v}}^{'} \end{matrix}$

である。したがって、衝突後の運動エネルギー $K'$ は

<5-53>　(5.4.7)　 $\begin{matrix} K' = \frac{m_{1}}{2} {\vec{v}}_{1}^{'2} + \frac{m_{2}}{2} {\vec{v}}_{2}^{'2} \\ = \frac{M}{2} {\vec{V}}^{'2} + \frac{μ}{2} {\vec{v}}^{'2} \end{matrix}$

となる。
　衝突前後の全運動量はどのような場合も変わらない。(5.1.3)式と(5.1.6)式から、衝突前後に $2$ 質点が持つ全運動量は<5-54> $(\vec{P} = m_{1} {\vec{v}}_{1} + m_{2} {\vec{v}}_{2} = M \vec{V})$ および<5-55> $({\vec{P}}^{'} = m_{1} {\vec{v}}_{1}^{'} + m_{2} {\vec{v}}_{2}^{'} = M {\vec{V}}^{'})$ であり、それが変わらないので $\vec{P} = {\vec{P}}^{'}$ であるから、よって $\vec{V} = {\vec{V}}^{'}$ である。ゆえに(5.4.7)式は

<5-56>　(5.4.8)　 $K' = \frac{M}{2} {\vec{V}}^{2} + \frac{μ}{2} {\vec{v}}^{'2}$

となる。
　もし衝突によってエネルギーが失われるとすれば、失われたエネルギーは衝突前に２質点が持っていたエネルギー $K$ と衝突後に２質点が持っているエネルギー $K^{'}$ の差 $(K - K')$ である。したがって $(K - K')$ が $0$ であれば衝突前に二つの物体が持っていたエネルギーはまったく失われず、もし $0$ でなければ、その量のエネルギーが衝突を通じ両物体の構成分子に分配される。そして場合によっては、そのエネルギーによって分子をつなぎとめている力が断ち切られ、物体がバラバラになることもある。衝突によるエネルギー変化 $(K - K')$ は(5.4.4)式と(5.4.8)式の差で与えられ、

<5-57>　(5.4.9)　 $K - K^{'} = \frac{μ}{2} {\vec{v}}^{2} [1 - \frac{({\vec{v}}_{1}^{'} - {\vec{v}}_{2}^{'})^{2}}{({\vec{v}}_{1} - {\vec{v}}_{2})^{2}}]$

と計算される。したがって右辺かっこの中の二項目がもし $1$ であれば、衝突によって運動エネルギーが失われることはないが、それが小さくなるにしたがって失われるエネルギーが大きくなる。したがって $e$ が $1$ からどの程度小さくなるかで、衝突によって失われるエネルギーの大きさがわかる。(5.4.9)式の中のそれを表す量

<5-58>　(5.4.10)　 $e = \frac{| {\vec{v}}_{1}^{'} - {\vec{v}}_{2}^{'} |}{| {\vec{v}}_{1} - {\vec{v}}_{2} |}$

を「衝突のはね返り係数」あるいは「衝突の反発係数」という[5]。これを使うと、(5.4.9)式は

<5-59>　(5.4.11)　 $K - K' = \frac{μ}{2} (1 - e^{2})$

と書かれる。 $e$ は絶対値の割り算であるから負になることはなく、また衝突によって失われるエネルギーは $2$ つの質点が衝突前に持っていたエネルギーを越えることはないので（すなわち、必ず $K - K' \geq 0$ なので）、(5.4.9)式より

<5-60>　(5.4.12)　 $0 \leq e \leq 1$

である。衝突によってエネルギーがまったく失われない場合、すなわち $K = K' (\to e = 1)$ である衝突を「弾性衝突」という。それに対してエネルギーが失われる衝突 $(K' < K)$ すなわち $e < 1$ である衝突を「非弾性衝突」という[6]。
　(5.4.10)式は、高校で学んだ、直線上を運動し衝突する二つの物体の「衝突公式」

<5-61>　(5.4.13)　 $e = - \frac{v_{1}' - v_{2}'}{v_{1} - v_{2}}$

と同じ式である。暗記するときに符号を間違えないようずいぶん苦労したと思う。 $e$ が元々持つ意味（衝突によって失われるエネルギーの大きさを表す量）と、(5.4.13)式の原形である(5.4.10)式に立ち帰れば、余計な符号をつけた(5.4.13)式を暗記する必要はまったくない。衝突で重要なことは、衝突の過程を通してエネルギーが失われるか否かに関係がなく必ず成り立つ「運動量保存則」が重要な役割を果たしていることである。
　(5.4.10)式と衝突の公式(5.4.13)式が同等であることを、同じ質量 $m$ を持つ２物体が摩擦のない直線上で起こす弾性衝突 $(e = 1)$ と、非弾性衝突 $(e = 0)$ の両極端な場合について確かめよう。直線上で衝突する２物体の衝突前の速度が $v_{1}$ と $v_{2}$ 、衝突後の速度が $v_{1}^{'}$ と $v_{2}^{'}$ であるから、運動量保存則は

<5-62>　(5.4.14)　 $\begin{matrix} m v_{1} + m v_{2} = m v_{1}^{'} + m v_{2}^{'} \\ \Rightarrow v_{1} + v_{2} = v_{1}^{'} + v_{2}^{'} \end{matrix}$

を与える。またエネルギー保存則は、もし衝突が弾性衝突 $(e = 1)$ なら $K = K^{'}$ であるから(5.4.4)式と(5.4.7)式から

<5-63>　(5.4.15)　 $\begin{matrix} \frac{1}{2} m v_{1}^{2} + \frac{1}{2} m v_{2}^{2} = \frac{1}{2} m v_{1}^{' 2} + \frac{1}{2} m v_{2}^{' 2} \\ \Rightarrow v_{1}^{2} + v_{2}^{2} = v_{1}^{' 2} + v_{2}^{' 2} \end{matrix}$

であり、もし衝突が完全な非弾性衝突 $(e = 0)$ なら(5.4.10)式より

<5-64>　(5.4.16)　 $v_{1}^{'} = v_{2}^{'}$

である。
　弾性衝突の場合は、(5.4.15)式で得た結論を

<5-65>　 $(v_{1} + v_{2})^{2} - 2 v_{1} v_{2} = (v_{1}^{'} + v_{2}^{'})^{2} - 2 v_{1}^{'} v_{2}^{'}$

と書き換えて、衝突が弾性か非弾性かに関係なく成り立つ(5.4.14)式の運動量保存則を使えば、関係式

<5-66>　(5.4.17)　 $v_{1} v_{2} = v_{1}^{'} v_{2}^{'}$

を得る。この式の両辺に $2$ をかけて、それを(5.4.15)式の最後の等式両辺から引き算すれば、

<5-67>　 $(v_{1} - v_{2})^{2} = (v_{1}^{'} - v_{2}^{'})^{2}$

を得る。この式は次の二つの場合に成り立つ：

<5-68>　(5.4.18)　 $\{\begin{matrix} (1) v_{1} - v_{2} = v_{1}^{'} - v_{2}^{'} \\ (2) v_{1} - v_{2} = - (v_{1}^{'} - v_{2}^{'}) \end{matrix}$

(1)の場合は、これを運動量保存則の結論(5.4.14)式と組み合わせると $v_{1} = v_{1}^{'}$ および $v_{2} = v_{2}^{'}$ となり、衝突前後の $2$ 物体の速度に何の変化もない結果が得られる。二つの物体の運動状態が衝突前後で変わらないということは、慣性の法則によって $2$ 物体の間に力が働かなかったことを意味し、すなわち実際には衝突が生じなかったことを意味する。数学的には、衝突が起きないときにも運動量保存則とエネルギー保存則が成り立つため、弾性衝突に対する代数的な条件がこのような解を必ず含むことによる。したがって衝突が起きたことを前提とする今の場合には、これは意味のない結論である。意味のある結論はしたがって $(2)$ の場合であり、明らかにそれは $(v_{1} - v_{2})$ と $(v_{1}^{'} - v_{2}^{'})$ の一方が正なら他方が負であることを意味しており、したがって、(5.4.10)式と(5.4.13)式は同じ内容を表わしている。
　もし衝突が完全な非弾性衝突（ $e = 0$ ）なら(5.4.16)式からわかるように、衝突後、両物体は同じ速度で動く。つまり完全な非弾性衝突を起こした物体は合体して運動する。柔らかい二つの粘土のかたまりを正面衝突させたことを想像すればよい。両者が合体した場合 $(v_{1}' = v_{2}')$ であっても衝突前後の全運動量は等しくなければならない。したがって

<5-69>　(5.4.19)　 $\begin{matrix} m v_{1} + m v_{2} = m v_{1}^{'} + m v_{2}^{'} \\ = 2 m v_{1}^{'} \\ = 2 m v_{2}^{'} \end{matrix}$

であるから

<5-70>　(5.4.20)　 $v_{1}^{'} = v_{2}^{'} = \frac{v_{1} + v_{2}}{2}$

であり、合体した後で両物体は衝突前に質量中心が持っていた速度、すなわち(5.4.2)式で $m_{1} = m_{2} = m$ としたときの $V$ と同じ速度で一体となって動く。

[1] 軽いＡと重いＢが「作用・反作用の法則」にしたがう力を及ぼしあうとき、場合によっては他方から受ける力の影響を考えなくてもよいのは重い物体（Ｂ）の方であり、ＡとＢが大きいか小さいかには関係がない。後に分かるように、これは力に「作用・反作用の法則」があることによって現れる「運動量保存の法則」の結論である。

[2] 時々、「作用・反作用の法則」に従わないかのようにみえる現象が身の周りにあるが、注意深くかつ微視的に考えれば、それらもやはり「作用・反作用の法則」に従う。自然界で「作用・反作用の法則」に従わない力はこれまで知られていない。

[3] 本来なら $Ω$ と $ω$ を「角速度」と呼ぶべきかもしれないが、慣習的にそれらを「振動数」という言葉で呼んでいる。一般に、角速度 $ω$ とそれに対応する振動数 $ν$ とは $ω = 2 πν$ によって関係づけられている。

[4] 二つの物体が衝突するとき、接近した物体間に働く力は二つの物体を構成する分子の間に働く力（分子間力）である。一般に分子間力は、二つの分子が離れているときは働かないが、それらが近づくにしたがって互いに弱く引きつけはじめ、分子がある距離まで接近すると、それ以上の接近を阻む強い反発力に変わる。そのなかで、ここでの衝突に関係するのは近い距離で働く強い反発力である。この強い反発力の作用が、節の冒頭で述べた「あたかも物体が接触して急激に運動状態が変わる」ことの力学的意味である。

[5] 右辺の分母と分子にあるベクトル量の絶対値はそのベクトルの大きさを表す。すなわちベクトル $\vec{a}$ の大きさ $| \vec{a} |$ は、 $\vec{a}$ の内積を使って <5-71> $(| \vec{a} | = \sqrt{\vec{a} \cdot \vec{a}})$ と与えられるか、あるいは $\vec{a}$ の直交座標成分を $(a_{x}, a_{y}, a_{z})$ とすれば <5-72> $(| \vec{a} | = \sqrt{a_{x}^{2} + a_{y}^{2} + a_{z}^{2}})$ で与えられる。

[6] 「弾性衝突」を「完全弾性衝突」とよぶ教科書があるが、「弾性衝突」と「完全弾性衝突」は明確に異なる意味を持っているので区別しなければならない。すなわち、「弾性衝突」は衝突前後の運動エネルギーが変わらない衝突を総称する言葉であり、衝突によって物体の変形や構造の変化が生じる場合も含んでいる。一方、「完全弾性衝突」は衝突前後の運動エネルギーが変わらないことに加えて、物体の形状や構造が衝突の前後で全く変わらない場合に用いられる。